题目内容
已知函数f(x)=ax+ (a>1),判断f(x)=0的根的个数.
(a>1),判断f(x)=0的根的个数.
 (a>1),判断f(x)=0的根的个数.
(a>1),判断f(x)=0的根的个数.方程f(x)=0有且只有一个根
设f1(x)=ax (a>1),f2(x)=- ,则f(x)=0的解即为f1(x)=f2(x)的解,即为函数f1(x)与f2(x)图象交点的横坐标.在同一坐标系中,作出函数f1(x)=ax(a>1)与f2(x)=-
,则f(x)=0的解即为f1(x)=f2(x)的解,即为函数f1(x)与f2(x)图象交点的横坐标.在同一坐标系中,作出函数f1(x)=ax(a>1)与f2(x)=-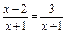 -1的图象(如图所示).
-1的图象(如图所示).
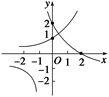
两函数图象有且只有一个交点,即方程f(x)=0有且只有一个根.
 ,则f(x)=0的解即为f1(x)=f2(x)的解,即为函数f1(x)与f2(x)图象交点的横坐标.在同一坐标系中,作出函数f1(x)=ax(a>1)与f2(x)=-
,则f(x)=0的解即为f1(x)=f2(x)的解,即为函数f1(x)与f2(x)图象交点的横坐标.在同一坐标系中,作出函数f1(x)=ax(a>1)与f2(x)=-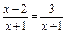 -1的图象(如图所示).
-1的图象(如图所示).
两函数图象有且只有一个交点,即方程f(x)=0有且只有一个根.

练习册系列答案
相关题目
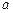 是使表达式
是使表达式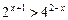 成立的最小整数,则方程
成立的最小整数,则方程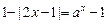 实数根的个数为( )
实数根的个数为( )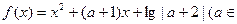
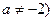
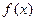 能表示成一个奇函数
能表示成一个奇函数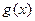 和一个偶函数
和一个偶函数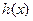 的和,求
的和,求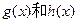 的解析式;
的解析式;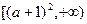 上是增函数与命题Q:.函数
上是增函数与命题Q:.函数 集体改饮某品牌的桶装纯净水,则年总费用由两部分组
集体改饮某品牌的桶装纯净水,则年总费用由两部分组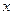 的方程
的方程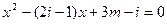 有实根,则实数
有实根,则实数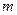 的值是(
的值是(  )
)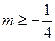
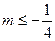
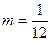

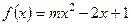 有且仅有一个正实数的零点,则实数
有且仅有一个正实数的零点,则实数 的取值范围是 .
的取值范围是 .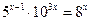 的解集是( ).
的解集是( ).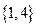 B.
B.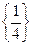 C.
C.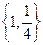 D
D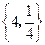
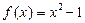 ,则函数
,则函数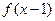 的零点是__________.
的零点是__________.