题目内容
给出下面四个命题:①函数y=x2-5x+4(-1≤x≤1)的最大值为10,最小值为-![]() ;
;
②函数y=2x2-4x+1(-2<x<4)的最大值为17,最小值为-1;
③函数y=x3-12x(-3<x<3)的最大值为16,最小值为-16;
④函数y=x3-12x(-2<x<2)既无最大值,也无最小值.
其中正确命题的个数有( )
A.1个 B.2个 C.3个 D.4个
解析:①y′=2x-5,令y′=0,得x=![]() ,但x∈[-1,1],舍去.又函数f(x)在区间的端点值为f(-1)=10,f(1)=0.
,但x∈[-1,1],舍去.又函数f(x)在区间的端点值为f(-1)=10,f(1)=0.
∴f(x)max=10,f(x)min=0.∴①错误.
②f′(x)=4x-4,令f′(x)=0,得x=1.
若x∈(1,4),则f′(x)>0,
若x∈(-2,1),则f′(x)<0.
∴x=1是函数f(x)的极小值点,也是函数f(x)的最小值.
∴f(x)min=f(1)=-1.
可知f(x)无最大值.∴②错误.
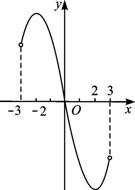
③f′(x)=3x2-12=3(x2-4),
令f′(x)=0,得x=-2或x=2.
∴x=2和x=-2是函数f(x)的极值点,且f(2)=23-24=-16,f(-2)=-23+24=16.
又f(3)=-9,f(-3)=9,其图象如图所示.
由图象可得出
f(x)max=f(-2)=16,
f(x)min=f(2)=-16.
④f′(x)=3x2-12=3(x2-4).
令f′(x)=0,得x=2或x=-2.
但x∈(-2,2),
∴上述方程无解.∴函数f(x)在(-2,2)上既无最大值,也无最小值.
答案:B

练习册系列答案
相关题目