题目内容
已知关于 的不等式
的不等式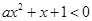 的解集不是空集,则实数
的解集不是空集,则实数 的取值范围是
的取值范围是
A.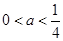 | B.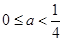 | C.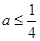 | D.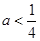 |
D
解析试题分析:因为关于 的不等式
的不等式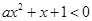 的解集为空集时,则要对于参数a是否为零来分为两种情况讨论,那么可知当a=0时,则有1<0,显然不成立。当a
的解集为空集时,则要对于参数a是否为零来分为两种情况讨论,那么可知当a=0时,则有1<0,显然不成立。当a 时,则开口向上,判别式小于等于零时,即a>0,且1-4a
时,则开口向上,判别式小于等于零时,即a>0,且1-4a ,解得
,解得 ,那么可知交集不为空集是的参数a的范围是
,那么可知交集不为空集是的参数a的范围是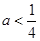 ,故选D.
,故选D.
考点:本试题主要考查了一元二次不等式的解集问题的运算。
点评:易错点是对于参数a的分类讨论不全,解决该试题的关键是能利用对立的思想来分析和求解当解集为空集时参数a的范围,进而得到不为空集时的范围。

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
不等式 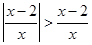 的解集是( )
的解集是( )
A.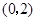 | B.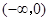 | C.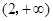 | D.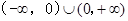 |
设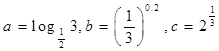 ,则( )
,则( )
A.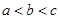 | B.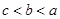 | C.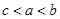 | D.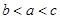 |
(文)设x∈R,[x]表示不大于x的最大整数,如:[π]=3,[-1.2]= ,[0.5]=0,则使[x2-1]=3的x的取值范围是
,[0.5]=0,则使[x2-1]=3的x的取值范围是
A.[2,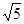 ) ) | B.(-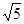 ,-2] ,-2] |
C.(-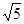 ,-2] ∪[2, ,-2] ∪[2,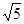 ) ) | D.[-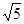 ,-2] ∪[2, ,-2] ∪[2,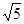 ] ] |
当a<0时,不等式42x2+ax-a2<0的解集为( )
A.{x| <x<- <x<-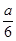 } } | B.{x|-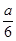 <x< <x< } } |
C.{x| <x<- <x<-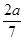 } } | D.空集 |
已知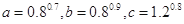 ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )
| A.c>a>b | B.b>a>c | C.c>b>a | D.a>b>c |
已知函数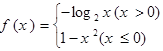 ,则不等式
,则不等式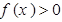 的解集为( )
的解集为( )
A.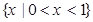 | B.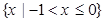 |
C.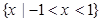 | D.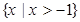 |
 的解集是( )
的解集是( )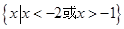 B
B 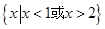
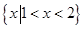 D.
D.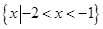
 的图象经过点A(1,1),则不等式
的图象经过点A(1,1),则不等式 的解集为______.
的解集为______.