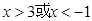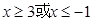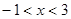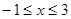题目内容
(文)设x∈R,[x]表示不大于x的最大整数,如:[π]=3,[-1.2]= ,[0.5]=0,则使[x2-1]=3的x的取值范围是
,[0.5]=0,则使[x2-1]=3的x的取值范围是
A.[2,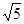 ) ) | B.(-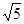 ,-2] ,-2] |
C.(-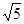 ,-2] ∪[2, ,-2] ∪[2,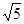 ) ) | D.[-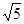 ,-2] ∪[2, ,-2] ∪[2,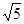 ] ] |
C
解析试题分析:由[x]定义可知 ,
,
所以x的取值范围为(-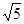 ,-2] ∪[2,
,-2] ∪[2,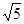 ).
).
考点:解一元二次不等式.
点评:本小题是新定义的题目,关键是搞清楚[x]中x的取值范围为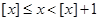 .
.

练习册系列答案
相关题目
若不等式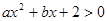 的解集为
的解集为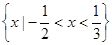 ,则a-b值是( )
,则a-b值是( )
| A.-10 | B.-14 | C.10 | D.14 |
已知关于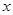 的不等式
的不等式 的解集为
的解集为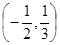 ,则
,则 的值是( )
的值是( )
| A.10 | B.-10 | C.14 | D.-14 |
已知关于 的不等式
的不等式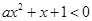 的解集不是空集,则实数
的解集不是空集,则实数 的取值范围是
的取值范围是
A.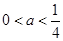 | B.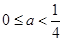 | C.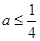 | D.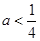 |
设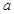 、
、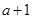 、
、 为钝角三角形的边,则
为钝角三角形的边,则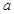 的取值范围是 ( )
的取值范围是 ( )
| A.0<a<3 | B.3<a<4 | C.1<a<3 | D.4<a<6 |
已知不等式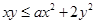 ,若对任意
,若对任意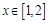 及
及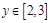 ,该不等式恒成立,则实数
,该不等式恒成立,则实数 的范围是( )
的范围是( )
A.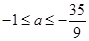  | B.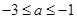 |
C. | D.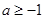 |
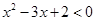 的解集为( )
的解集为( )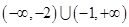 B.
B.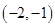
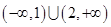 D.
D.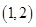
 的解集是_____ ___.
的解集是_____ ___.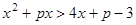 都成立的x的取
都成立的x的取