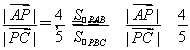题目内容
已知点P在△ABC所在的平面内,若2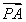 +3
+3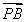 +4
+4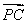 =3
=3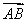 ,则△PAB与△PBC的面积的比值为__________.
,则△PAB与△PBC的面积的比值为__________.
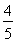
【解析】由2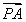 +3
+3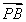 +4
+4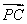 =3
=3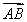 ,得2
,得2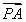 +4
+4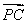 =3
=3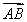 +3
+3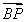 ,∴2
,∴2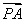 +4
+4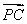 =3
=3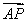 ,即4
,即4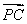 =5
=5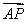 .
.
∴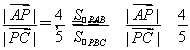

练习册系列答案
相关题目
题目内容
已知点P在△ABC所在的平面内,若2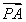 +3
+3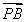 +4
+4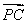 =3
=3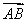 ,则△PAB与△PBC的面积的比值为__________.
,则△PAB与△PBC的面积的比值为__________.
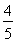
【解析】由2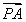 +3
+3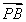 +4
+4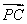 =3
=3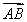 ,得2
,得2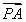 +4
+4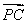 =3
=3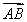 +3
+3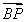 ,∴2
,∴2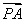 +4
+4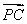 =3
=3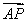 ,即4
,即4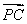 =5
=5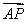 .
.
∴