题目内容
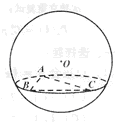
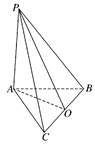
如图,在半径为3的球面上有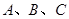 三点,
三点,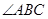 =90°,
=90°,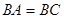 ,球心O到平面
,球心O到平面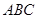 的距离是
的距离是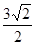 ,则
,则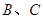 两点的球面距离是
两点的球面距离是
 三点,
三点,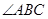 =90°,
=90°,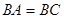 ,球心O到平面
,球心O到平面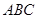 的距离是
的距离是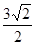 ,则
,则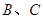 两点的球面距离是
两点的球面距离是 
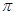
分析:欲求B、C两点的球面距离,即要求出球心角∠BOC,将其置于三角形BOC中解决.
解:∵AC是小圆的直径.
所以过球心O作小圆的垂线,垂足O’是AC的中点.
O’C=
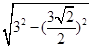
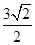 =,AC="3"
=,AC="3" 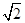 ,
,∴BC=3,即BC=OB=OC.∴∠BOC=
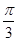 ,
,则B、C两点的球面距离=
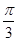
×3=π.
故答案为:π.

练习册系列答案
相关题目
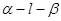 ,点
,点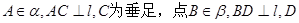 为垂足,若
为垂足,若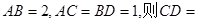 ( )
( )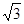
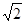
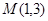 ,
,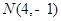 ,则
,则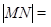 ___________.
___________.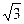 米,则甲乙两人相距 米。
米,则甲乙两人相距 米。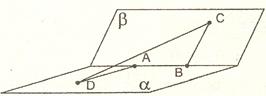
 =" " 时,直线
=" " 时,直线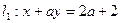 ,直线
,直线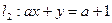 平行.
平行.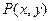 在直线
在直线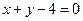 上,则
上,则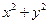 的最小值是________________.
的最小值是________________.