题目内容
已知圆C1:x2+y2+D1x+8y-8=0,圆C2:x2+y2+D2x-4y-2=0.(1)若D1=2,D2=-4,求圆C1与圆C2的公共弦所在的直线l1的方程;
(2)在(1)的条件下,已知P(-3,m)是直线l1上一点,过点P分别作直线与圆C1、圆C2相切,切点为A、B,求证:|PA|=|PB|;
(3)将圆C1、圆C2的方程相减得一直线l2:(D1-D2)x+12y-6=0.Q是直线l2上,且在圆C1、圆C2外部的任意一点.过点Q分别作直线QM、QN与圆C1、圆C2相切,切点为M、N,试探究|QM|与|QN|的关系,并说明理由.
【答案】分析:(1)对两圆的方程作差即可得出两圆的公共弦所在的直线方程.
(2)求出两个圆的圆心坐标与半径,求出两个切线长即可证明结果.
(3)求出两个圆的圆心坐标与半径,利用切线长与半径的垂直关系,比较|QM|与|QN|的关系.
解答:解:(1)由题意,∵D1=2,D2=-4,
∴圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x-4y-2=0相交,
∴两圆的方程作差得6x+12y-6=0,
即公式弦所在直线方程为x+2y-1=0.
(2)P(-3,m)是直线l1上一点,所以m=2
过点P分别作直线与圆C1、圆C2相切,切点为A、B,
圆C1的圆心坐标(-1,-4),半径为:5;
圆C2的圆心坐标(2,2),半径为: .
.
所以PA2=(-1+3)2+(-4-2)2-25=15.
PB2=(2+3)2+(2-2)2-10=15.
所以|PA|=|PB|;
(3)圆C1x2+y2+D1x+8y-8=0,圆心坐标( ,-4),半径为:
,-4),半径为: ;
;
圆C2:x2+y2+D2x-4y-2=0,圆心坐标( ,2),半径为:
,2),半径为: .
.
直线l2:(D1-D2)x+12y-6=0.Q是直线l2上,设Q(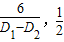 ),
),
|QM|2= 与|QN|2=
与|QN|2= ,
,
|QM|2-|QN|2= ,
,
当 时,|QM|=|QN|,
时,|QM|=|QN|,
当 时,|QM|>|QN|,
时,|QM|>|QN|,
当 时,|QM|<|QN|.
时,|QM|<|QN|.
点评:本题考查圆的方程的综合应用与圆的位置关系,考查发现问题与解决问题的能力.
(2)求出两个圆的圆心坐标与半径,求出两个切线长即可证明结果.
(3)求出两个圆的圆心坐标与半径,利用切线长与半径的垂直关系,比较|QM|与|QN|的关系.
解答:解:(1)由题意,∵D1=2,D2=-4,
∴圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x-4y-2=0相交,
∴两圆的方程作差得6x+12y-6=0,
即公式弦所在直线方程为x+2y-1=0.
(2)P(-3,m)是直线l1上一点,所以m=2
过点P分别作直线与圆C1、圆C2相切,切点为A、B,
圆C1的圆心坐标(-1,-4),半径为:5;
圆C2的圆心坐标(2,2),半径为:
 .
.所以PA2=(-1+3)2+(-4-2)2-25=15.
PB2=(2+3)2+(2-2)2-10=15.

所以|PA|=|PB|;
(3)圆C1x2+y2+D1x+8y-8=0,圆心坐标(
 ,-4),半径为:
,-4),半径为: ;
;圆C2:x2+y2+D2x-4y-2=0,圆心坐标(
 ,2),半径为:
,2),半径为: .
.直线l2:(D1-D2)x+12y-6=0.Q是直线l2上,设Q(
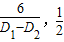 ),
),|QM|2=
 与|QN|2=
与|QN|2= ,
,|QM|2-|QN|2=
 ,
,当
 时,|QM|=|QN|,
时,|QM|=|QN|,当
 时,|QM|>|QN|,
时,|QM|>|QN|,当
 时,|QM|<|QN|.
时,|QM|<|QN|.点评:本题考查圆的方程的综合应用与圆的位置关系,考查发现问题与解决问题的能力.

练习册系列答案
相关题目
 (2013•宁波模拟)如图,已知圆
(2013•宁波模拟)如图,已知圆