题目内容
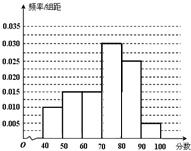 从参加高三年级期中考试的学生中随机抽出40名学生,将其数学成绩(均为整数)分成六组[40,50),[50,60),…[90,100]后得到如下频率分布直方图.
从参加高三年级期中考试的学生中随机抽出40名学生,将其数学成绩(均为整数)分成六组[40,50),[50,60),…[90,100]后得到如下频率分布直方图.(Ⅰ)同一组数据用该组区间的中点值作为代表,据此估计本次考试的平均分;
(Ⅱ)从上述40名学生中随机抽取2人,求这2人成绩都在[70,80)的概率;
(Ⅲ)从上述40名学生中随机抽取2人,抽到的学生成绩在[40,60),记为0分,在[60,100],记为1分.用X表示抽取结束后的总记分,求X的分布列和数学期望.
分析:(I)根据平均数是频率分布直方图各个小矩形的面积×底边中点横坐标之和,求出本次考试的平均分;
(II)先求出成绩在[70,80)的人数,然后利用概率公式进行求解即可;
(III)先分别求出学生成绩在[40,60),在[60,100]的人数,X的所以可能取值为0,1,2,列出分布列,最后利用数学期望公式进行求解即可.
(II)先求出成绩在[70,80)的人数,然后利用概率公式进行求解即可;
(III)先分别求出学生成绩在[40,60),在[60,100]的人数,X的所以可能取值为0,1,2,列出分布列,最后利用数学期望公式进行求解即可.
解答:解:(Ⅰ)
=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71
据此估计本次考试的平均分为71.(3分)
(Ⅱ)成绩在[70,80)的有12人(4分)
P=
=
从这40名学生中抽取2人,这2人成绩都在[70,80)的概率为
(Ⅲ)学生成绩在[40,60)的有10人,在[60,100]的有30人,X的所以可能取值为0,1,2(8分)
则P(X=0)=
=
P(X=1)=
=
P(X=2)=
=
(每个1分)(11分)
所以X的分布列为 (12分)
(12分)
数学期望EX=0×
+1×
+2×
=1.5
. |
| x |
据此估计本次考试的平均分为71.(3分)
(Ⅱ)成绩在[70,80)的有12人(4分)
P=
| ||
|
| 11 |
| 130 |
从这40名学生中抽取2人,这2人成绩都在[70,80)的概率为
| 11 |
| 130 |
(Ⅲ)学生成绩在[40,60)的有10人,在[60,100]的有30人,X的所以可能取值为0,1,2(8分)
则P(X=0)=
| ||
|
| 3 |
| 52 |
| ||||
|
| 5 |
| 13 |
| ||
|
| 29 |
| 52 |
所以X的分布列为
 (12分)
(12分)数学期望EX=0×
| 3 |
| 52 |
| 5 |
| 13 |
| 29 |
| 52 |
点评:本题考查频率分布直方图的相关知识,以及概率和数学期望等有关基础知识,属于中档题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
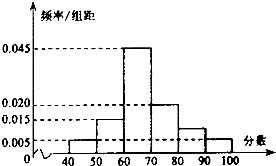 (2013•济宁一模)某校从参加高三年级期中考试的学生中随机统计了40名学生的政治成绩,这40名学生的成绩全部在40分至l00分之间,据此绘制了如图所示的样本频率分布直方图.
(2013•济宁一模)某校从参加高三年级期中考试的学生中随机统计了40名学生的政治成绩,这40名学生的成绩全部在40分至l00分之间,据此绘制了如图所示的样本频率分布直方图. 某校从参加高三年级期中考试的学生中随机选取40名学生,并统计了他们的政治成绩,这40名学生的政治成绩全部在40分至100分之间,现将成绩分成以下6段:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],据此绘制了如图所示的频率分布直方图.
某校从参加高三年级期中考试的学生中随机选取40名学生,并统计了他们的政治成绩,这40名学生的政治成绩全部在40分至100分之间,现将成绩分成以下6段:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],据此绘制了如图所示的频率分布直方图.