��Ŀ����
������Բ ����Բ����ԭ��O���뾶Ϊ
����Բ����ԭ��O���뾶Ϊ ��Բ����ԲC�ġ�Բ��������ԲC��һ������Ϊ
��Բ����ԲC�ġ�Բ��������ԲC��һ������Ϊ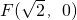 ��������ϵ�һ���˵㵽F�ľ���Ϊ
��������ϵ�һ���˵㵽F�ľ���Ϊ ��
��
��I������ԲC�ķ��̺��䡰Բ�����̣���II����P����ԲC�ġ�Բ���ϵ�һ�����㣬����P��ֱ��l1��l2��ʹ��l1��l2����ԲC��ֻ��һ�����㣬��l1��l2�ֱ��䡰Բ���ڵ�M��N��
�ٵ�PΪ��Բ����y��������Ľ���ʱ����l1��l2�ķ��̣�
����֤��|MN|Ϊ��ֵ��
�⣺��I����Ϊ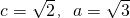 ������b=1
������b=1
������Բ�ķ���Ϊ ��
��
Բ�ķ���Ϊx2+y2=4��
��II����1����ΪԲx2+y2=4��y��������Ľ���ΪP��0��2����
�����P��0��2����������Բ��һ���������ֱ��Ϊy=kx+2��
����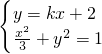 ����ȥy���õ���1+3k2��x2+12kx+9=0��
����ȥy���õ���1+3k2��x2+12kx+9=0��
��Ϊ��Բ��y=kx+2ֻ��һ�������㣬
���ԡ�=144k2-4��9��1+3k2��=0��
���k=��1��
����l1��l2����Ϊy=x+2��y=-x+2��
��2���ٵ�l1��l2����һ����б��ʱ��������l1��б�ʣ�
��Ϊl1����Բֻ��һ�������㣬���䷽��Ϊ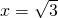 ��
��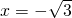 ��
��
��l1����Ϊ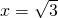 ʱ����ʱl1��Բ���ڵ�
ʱ����ʱl1��Բ���ڵ�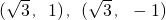 ��
��
��ʱ������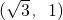 ����
����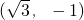 ��������Բֻ��һ���������ֱ����y=1����y=-1������l2Ϊy=1����y=-1������Ȼֱ��l1��l2��ֱ��
��������Բֻ��һ���������ֱ����y=1����y=-1������l2Ϊy=1����y=-1������Ȼֱ��l1��l2��ֱ��
ͬ����֤l1����Ϊ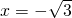 ʱ��ֱ��l1��l2��ֱ��
ʱ��ֱ��l1��l2��ֱ��
�ڵ�l1��l2����б��ʱ�����P��x0��y0��������x02+y02=4��
�辭����P��x0��y0������Բֻ��һ���������ֱ��Ϊy=t��x-x0��+y0��
��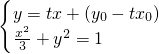 ����ȥy�õ�x2+3��tx+��y0-tx0����2-3=0��
����ȥy�õ�x2+3��tx+��y0-tx0����2-3=0��
����1+3t2��x2+6t��y0-tx0��x+3��y0-tx0��2-3=0����=[6t��y0-tx0��]2-4•��1+3t2��[3��y0-tx0��2-3]=0��
��������õ�����3-x02��t2+2x0y0t+1-y02=0��
��Ϊx02+y02=4�������У�3-x02��t2+2x0y0t+��x02-3��=0��
��l1��l2��б�ʷֱ�Ϊt1��t2����Ϊl1��l2����Բ��ֻ��һ�������㣬
����t1��t2�����������̣�3-x02��t2+2x0y0t+��x02-3��=0��
����t1•t2=-1����l1��l2��ֱ��
�ۺϢ٢�֪����Ϊl1��l2������P��x0��y0�����ֱַ���Բ�ڵ�M��N����l1��l2��ֱ��
�����߶�MNΪԲx2+y2=4��ֱ��������|MN|=4��
��������I������Բ�ķ�����Բ�ķ��̹�ϵ���Բ�ķ���
��II����1����Բx2+y2=4��y��������Ľ���ΪP��0��2����
����Բ��һ���������ֱ��Ϊy=kx+2����Բ��������������Բ��y=kx+2ֻ��һ�������㣬���k���Ӷ���l1��l2����
��2������������ٵ�l1��l2����һ����б�ʺ͢ڵ�l1��l2����б�ʴ�����
������������Ҫ����ֱ�������ߵ�λ�ù�ϵ��ͨ���龳���ã���չ��Բ���ߵ�Ӧ�÷�Χ��ͬʱ��������֪ʶ��������ѧ���ۺ�����֪ʶ��������
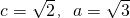 ������b=1
������b=1������Բ�ķ���Ϊ
 ��
��Բ�ķ���Ϊx2+y2=4��
��II����1����ΪԲx2+y2=4��y��������Ľ���ΪP��0��2����
�����P��0��2����������Բ��һ���������ֱ��Ϊy=kx+2��
����
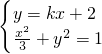 ����ȥy���õ���1+3k2��x2+12kx+9=0��
����ȥy���õ���1+3k2��x2+12kx+9=0����Ϊ��Բ��y=kx+2ֻ��һ�������㣬
���ԡ�=144k2-4��9��1+3k2��=0��
���k=��1��
����l1��l2����Ϊy=x+2��y=-x+2��
��2���ٵ�l1��l2����һ����б��ʱ��������l1��б�ʣ�
��Ϊl1����Բֻ��һ�������㣬���䷽��Ϊ
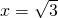 ��
��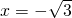 ��
����l1����Ϊ
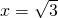 ʱ����ʱl1��Բ���ڵ�
ʱ����ʱl1��Բ���ڵ�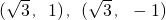 ��
����ʱ������
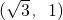 ����
����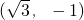 ��������Բֻ��һ���������ֱ����y=1����y=-1������l2Ϊy=1����y=-1������Ȼֱ��l1��l2��ֱ��
��������Բֻ��һ���������ֱ����y=1����y=-1������l2Ϊy=1����y=-1������Ȼֱ��l1��l2��ֱ��ͬ����֤l1����Ϊ
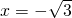 ʱ��ֱ��l1��l2��ֱ��
ʱ��ֱ��l1��l2��ֱ���ڵ�l1��l2����б��ʱ�����P��x0��y0��������x02+y02=4��
�辭����P��x0��y0������Բֻ��һ���������ֱ��Ϊy=t��x-x0��+y0��
��
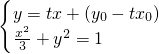 ����ȥy�õ�x2+3��tx+��y0-tx0����2-3=0��
����ȥy�õ�x2+3��tx+��y0-tx0����2-3=0������1+3t2��x2+6t��y0-tx0��x+3��y0-tx0��2-3=0����=[6t��y0-tx0��]2-4•��1+3t2��[3��y0-tx0��2-3]=0��
��������õ�����3-x02��t2+2x0y0t+1-y02=0��
��Ϊx02+y02=4�������У�3-x02��t2+2x0y0t+��x02-3��=0��
��l1��l2��б�ʷֱ�Ϊt1��t2����Ϊl1��l2����Բ��ֻ��һ�������㣬
����t1��t2�����������̣�3-x02��t2+2x0y0t+��x02-3��=0��
����t1•t2=-1����l1��l2��ֱ��
�ۺϢ٢�֪����Ϊl1��l2������P��x0��y0�����ֱַ���Բ�ڵ�M��N����l1��l2��ֱ��
�����߶�MNΪԲx2+y2=4��ֱ��������|MN|=4��
��������I������Բ�ķ�����Բ�ķ��̹�ϵ���Բ�ķ���
��II����1����Բx2+y2=4��y��������Ľ���ΪP��0��2����
����Բ��һ���������ֱ��Ϊy=kx+2����Բ��������������Բ��y=kx+2ֻ��һ�������㣬���k���Ӷ���l1��l2����
��2������������ٵ�l1��l2����һ����б�ʺ͢ڵ�l1��l2����б�ʴ�����
������������Ҫ����ֱ�������ߵ�λ�ù�ϵ��ͨ���龳���ã���չ��Բ���ߵ�Ӧ�÷�Χ��ͬʱ��������֪ʶ��������ѧ���ۺ�����֪ʶ��������

��ϰ��ϵ�д�
�����Ŀ
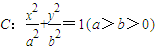 ����Բ����ԭ��O���뾶Ϊ
����Բ����ԭ��O���뾶Ϊ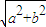 ��Բ����ԲC�ġ�Բ��������ԲC��һ������Ϊ
��Բ����ԲC�ġ�Բ��������ԲC��һ������Ϊ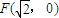 ��������ϵ�һ���˵㵽F�ľ���Ϊ
��������ϵ�һ���˵㵽F�ľ���Ϊ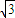 ��
��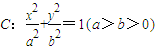 ����Բ����ԭ��O���뾶Ϊ
����Բ����ԭ��O���뾶Ϊ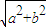 ��Բ����ԲC�ġ�Բ��������ԲC��һ������Ϊ
��Բ����ԲC�ġ�Բ��������ԲC��һ������Ϊ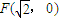 ��������ϵ�һ���˵㵽F�ľ���Ϊ
��������ϵ�һ���˵㵽F�ľ���Ϊ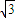 ��
��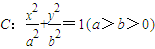 ����Բ����ԭ��O���뾶Ϊ
����Բ����ԭ��O���뾶Ϊ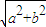 ��Բ����ԲC�ġ�Բ��������ԲC��һ������Ϊ
��Բ����ԲC�ġ�Բ��������ԲC��һ������Ϊ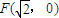 ��������ϵ�һ���˵㵽F�ľ���Ϊ
��������ϵ�һ���˵㵽F�ľ���Ϊ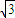 ��
��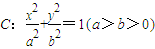 ����Բ����ԭ��O���뾶Ϊ
����Բ����ԭ��O���뾶Ϊ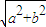 ��Բ����ԲC�ġ�Բ��������ԲC��һ������Ϊ
��Բ����ԲC�ġ�Բ��������ԲC��һ������Ϊ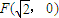 ��������ϵ�һ���˵㵽F�ľ���Ϊ
��������ϵ�һ���˵㵽F�ľ���Ϊ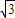 ��
��