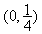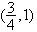题目内容
方程lgx+x=0的根所在区间是( )
分析:对各选项依次加以判断,得到只有B项可能正确.再根据函数单调性和零点存在性定理加以验证,即可得到本题答案.
解答:解:∵lgx有意义,必须x>0,
∴A项的区间(-∞,0)表示负数,故不正确,
又∵当x>1时,lgx>lg1=0,
∴由不等式的基本性质,可得lgx+x>0,
当x>1时,lgx+x是正数,不可能为0,因此C、D不正确,
综上所述,只有B项可能正确,事实上记F(x)=lgx+x
取x=0.1,可得lgx+x=-1+0.1=-0.9<0,取x=1,可得lgx+x=1>0
∴F(0.1)F(1)<0,
由函数零点存在性定理,可得在区间(0,1)上lgx+x=0必定有根
故选:B
∴A项的区间(-∞,0)表示负数,故不正确,
又∵当x>1时,lgx>lg1=0,
∴由不等式的基本性质,可得lgx+x>0,
当x>1时,lgx+x是正数,不可能为0,因此C、D不正确,
综上所述,只有B项可能正确,事实上记F(x)=lgx+x
取x=0.1,可得lgx+x=-1+0.1=-0.9<0,取x=1,可得lgx+x=1>0
∴F(0.1)F(1)<0,
由函数零点存在性定理,可得在区间(0,1)上lgx+x=0必定有根
故选:B
点评:本题给出含有对数的方程,求函数零点所在的区间,着重考查了函数单调性和零点存在性定理等知识,属于基础题.

练习册系列答案
相关题目