题目内容
已知点F椭圆E: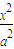 +
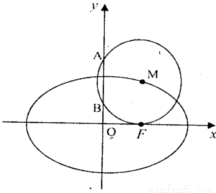
+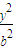 =1(a>b>0)的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且△ABM是边长为2的正三角形;又椭圆E上的P、Q两点关于直线l:y=x+n对称.
=1(a>b>0)的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且△ABM是边长为2的正三角形;又椭圆E上的P、Q两点关于直线l:y=x+n对称.(I)求椭圆E的方程;
(II)当直线l过点(0,
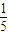 )时,求直线PQ的方程;
)时,求直线PQ的方程;(III)若点C是直线l上一点,且∠PCQ=
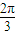 ,求△PCQ面积的最大值.
,求△PCQ面积的最大值.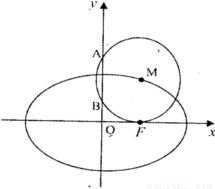
【答案】分析:(I)先利用△ABM是边长为2的正三角形求出c,再利用点M在椭圆E上即可求椭圆E的方程;
(II)把直线PQ的方程与椭圆方程联立求出P、Q两点的坐标之间的关系,再利用P、Q两点关于直线l:y=x+n对称.即可求直线PQ的方程;
(III)把△PCQ面积用|PQ|表示出来,再利用弦长公式求出|PQ|即可求△PCQ面积的最大值.
解答:解:(I)由题意可知:
M (c,2)且c为正三角形的高,所以c=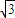
将点M坐标代入椭圆方程可得: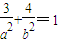 与a2=b2+3联立可得:a2=9,b2=6,所以椭圆方程为:
与a2=b2+3联立可得:a2=9,b2=6,所以椭圆方程为: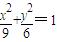
(II)设PQ:y=-x+m代入椭圆方程2x2+3y2=18整理得5x2-6mx+3m2-18=0
△=36m2-4•5•(3m2-18)>0,则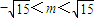
令P(x1,y1),Q(x2,y2),故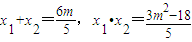
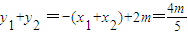 ,则P、Q的中点为
,则P、Q的中点为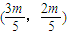
由于l方程为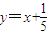 ,故
,故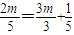 ,得m=-1
,得m=-1
则直线PQ的方程为y=-x-1
(III)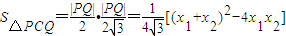 [1+(-1)2]
[1+(-1)2]
=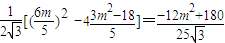
则当m=0时,S△POQ的最大值为
点评:本题是圆锥曲线的综合大题,主要考查解析几何的有关知识,以及分析问题与解决问题的能力.
(II)把直线PQ的方程与椭圆方程联立求出P、Q两点的坐标之间的关系,再利用P、Q两点关于直线l:y=x+n对称.即可求直线PQ的方程;
(III)把△PCQ面积用|PQ|表示出来,再利用弦长公式求出|PQ|即可求△PCQ面积的最大值.
解答:解:(I)由题意可知:
M (c,2)且c为正三角形的高,所以c=
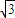
将点M坐标代入椭圆方程可得:
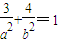 与a2=b2+3联立可得:a2=9,b2=6,所以椭圆方程为:
与a2=b2+3联立可得:a2=9,b2=6,所以椭圆方程为: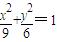
(II)设PQ:y=-x+m代入椭圆方程2x2+3y2=18整理得5x2-6mx+3m2-18=0
△=36m2-4•5•(3m2-18)>0,则
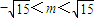
令P(x1,y1),Q(x2,y2),故
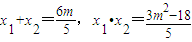
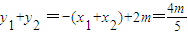 ,则P、Q的中点为
,则P、Q的中点为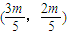
由于l方程为
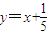 ,故
,故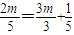 ,得m=-1
,得m=-1则直线PQ的方程为y=-x-1
(III)
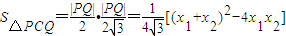 [1+(-1)2]
[1+(-1)2]=
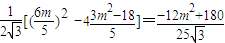
则当m=0时,S△POQ的最大值为

点评:本题是圆锥曲线的综合大题,主要考查解析几何的有关知识,以及分析问题与解决问题的能力.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
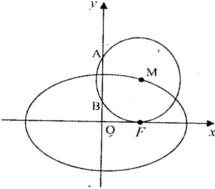 已知点F椭圆E:
已知点F椭圆E: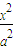 +
+ =1(a>b>0)的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且△ABM是边长为2的正三角形;又椭圆E上的P、Q两点关于直线l:y=x+n对称.
=1(a>b>0)的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且△ABM是边长为2的正三角形;又椭圆E上的P、Q两点关于直线l:y=x+n对称.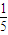 )时,求直线PQ的方程;
)时,求直线PQ的方程;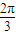 ,求△PCQ面积的最大值.
,求△PCQ面积的最大值.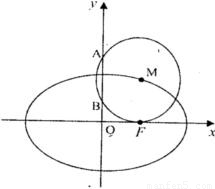
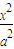 +
+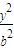 =1(a>b>0)的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且△ABM是边长为2的正三角形;又椭圆E上的P、Q两点关于直线l:y=x+n对称.
=1(a>b>0)的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且△ABM是边长为2的正三角形;又椭圆E上的P、Q两点关于直线l:y=x+n对称.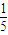 )时,求直线PQ的方程;
)时,求直线PQ的方程;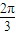 ,求△PCQ面积的最大值.
,求△PCQ面积的最大值.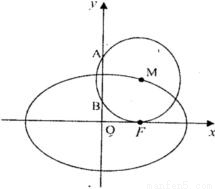
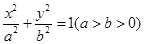 的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且
的右焦点,点M在椭圆E上,以M为圆心的圆与x轴切于点F,与y轴交于A、B两点,且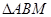 是边长为2的正三角形;又椭圆E上的P、Q两点关于直线
是边长为2的正三角形;又椭圆E上的P、Q两点关于直线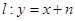 对称.
对称.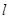 过点(
过点(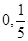 )时,求直线PQ的方程;
)时,求直线PQ的方程;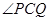 =
=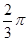 ,求
,求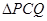 面积的最大值.
面积的最大值.