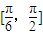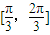题目内容
已知两条异面直线a与b所成的角为50°，P为空间一点，则过P点且与a，b所成的角都是30°的直线有且仅有( )
A．1条 B．2条 C．3条 D．4条
答案：B
解析：
解析：
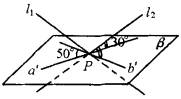
把直线a，b分别平移至经过P，即过P分别作直线a′∥a，b′∥b，这时a′、b′相交于点P，所成的两组对角分别等于50°和130°． 记a′、b′所确定的平面为b，那么在b平面内不存在与a′、b′都成30°的直线，故过P且与a′、b′成30°的直线必在平面b外，且在b内的射影必平分a′、b′所成的 50°的对顶角，这样的直线有且仅有两条，它们关于平面b对称．
|
练习册系列答案
相关题目
已知两条异面直线a，b所成的角为
，直线l与a，直线l与b所成的角为θ，则θ的范围是（ ）
| π |
| 3 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
β=c，则
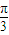，直线l与a，直线l与b所成的角为θ，则θ的范围是（ ）
