题目内容
已知函数
，函数
.
（1）当
时，求函数f(x)的最小值；
（2）设函数h(x)=(1－x)f(x)+16，试根据m的取值分析函数h(x)的图象与函数g(x)的图象交点的个数.
(1) x=4时，取等号，故函数f(x)的最小值为0.
（2）当
或
时，h(x)的图象与g(x)的图象恰有1个交点；
当
时，h(x)的图象与g(x)的图象恰有2个交点；
当
时，h(x)的图象与g(x(的图象恰有3个交点.
解析:
(1) 方法一： ∵ x>1 , 
，
当且仅当x=4时，取等号，故函数f(x)的最小值为0；
方法二：∵ x>1， 
当且仅当
即x=4时，取等号，故函数f(x)的最小值为0.
方法三：求导（略） ……………………………………4分
（2）由于h(x)=(1－x)f(x)+16=
设 F(x)=g(x)－h(x)= 
(
且
)，则
，……………………………6分
令
得x=3或x=1（舍）又∵
，
，
，F（3）＝6ln3－15+m
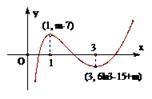
根据导数的符号及函数的单调情况、取极值的情况作出的草图如下：………………11分
由此可得：
当或时，h(x)的图象与g(x)的图象恰有1个交点；
当时，h(x)的图象与g(x)的图象恰有2个交点；
当时，h(x)的图象与g(x(的图象恰有3个交点.
练习册系列答案
名师金手指领衔课时系列答案
相关题目
已知函数f（x）的定义域为[-2，+∞），部分对应值如表格所示，f′（x）为f（x）．的导函数，函数y=f′（x）的图象如右图所示：