题目内容
(12分)已知函数![]() 在
在![]() 上是增函数。
上是增函数。
![]() (Ⅰ)求
(Ⅰ)求![]() 的取值范围;
的取值范围;
解析:(Ⅰ)![]() 。∵
。∵![]() 在(0,1)上 是增函数,
在(0,1)上 是增函数,
∴![]() 在(0,1)上恒成立,即
在(0,1)上恒成立,即![]()
∵![]() (当且仅当
(当且仅当![]() 时取等号),所以
时取等号),所以![]() 。
。
(Ⅱ)设![]() ,则
,则![]() (显然
(显然![]() )
)
当![]() 时,
时,![]() 在区间[1,3]上是增函数,所以h(t)的最小值为
在区间[1,3]上是增函数,所以h(t)的最小值为![]() 。
。
当![]() 时,
时,
因为函数h(t)在区间![]() 是增函数,在区间
是增函数,在区间![]() 是也是增函数,又h(t)在[1,3]上为连续函数,所以h(t)在[1,3]上为增函数,所以h(t)的最小值为h(1)=
是也是增函数,又h(t)在[1,3]上为连续函数,所以h(t)在[1,3]上为增函数,所以h(t)的最小值为h(1)=![]()


练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
 在
在 上是增函数,
上是增函数, ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 在
在 上是增函数,则
上是增函数,则 的最小值是 ( )
的最小值是 ( )
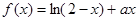 在
在 上是增函数,
上是增函数, 。当
。当 时,函数
时,函数 的最大值
的最大值 与最小值
与最小值 的差为
的差为 ,试求
,试求 的值。
的值。