题目内容
已知函数 在
在 上是增函数,
上是增函数, ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.
D.
【答案】
B
【解析】
试题分析:根据题意,由于函数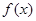 在
在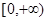 上是增函数,且函数y=f(|x|)是偶函数, 那么可知,在
上是增函数,且函数y=f(|x|)是偶函数, 那么可知,在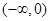 上是减函数,同时由于
上是减函数,同时由于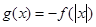 ,那么利用函数的对称变换可知,在在
,那么利用函数的对称变换可知,在在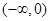 上是增函数,
上是增函数,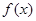 在
在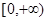 上是减函数,因此可知,要满足
上是减函数,因此可知,要满足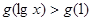 ,则只要
,则只要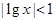 ,解得x的范围是
,解得x的范围是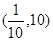 ,故选B.
,故选B.
考点:本试题考查抽象函数单调性。
点评:利用已知函数的单调性,结合偶函数的对称性,确定出g(x)的单调性是解决该试题的关键,并能利用对称性,找到满足不等式成立的条件,属于基础题。

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 在
在 上是增函数,则
上是增函数,则 的最小值是 ( )
的最小值是 ( )
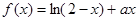 在
在 上是增函数,
上是增函数, 。当
。当 时,函数
时,函数 的最大值
的最大值 与最小值
与最小值 的差为
的差为 ,试求
,试求 的值。
的值。