题目内容
已知中心为O的正方形ABCD的边长为2,点M、N分别为线段BC、CD上的两个不同点,且|
|≤1,则
•
的取值范围是( )
. |
| MN |
. |
| OM |
. |
| ON |
分析:将正方体放入坐标系中,利用坐标法,结合数量积的定义和公式,转化为线性规划求
•
的取值范围.
. |
| OM |
. |
| ON |
解答: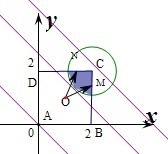 解:将正方体ABCD放入直角坐标系中,如图:则O(1,1),C(2,2),
解:将正方体ABCD放入直角坐标系中,如图:则O(1,1),C(2,2),
设M(2,y),N(x,2),则设z=
•
=(1,y-1)•(x-1,1)=x-1+y-1=x+y-2,
则y=-x+z+2,
∵|
|≤1,∴
≤1,
即(x-2)2+(y-2)2≤1,
平移直线y=-x+z+2,
由图象可知当直线经过点C(2,2)时,直线y=-x+z+2的截距最大,此时z=2-2+2=2,
当直线y=-x+z+2与圆相切时(圆下方),直线y=-x+z+2的截距最小,此时z最小.
直线一般式方程为x+y-2-z=0,
则圆心C到直线x+y-2-z=0的距离d=
=
=1,
解得z=2-
或z=2+
(舍去).
∵M、N是不同的两点,所以z无最大值,
∴2-
≤z<2.
即
•
的取值范围是[2-
,2).
故选B.
 解:将正方体ABCD放入直角坐标系中,如图:则O(1,1),C(2,2),
解:将正方体ABCD放入直角坐标系中,如图:则O(1,1),C(2,2),设M(2,y),N(x,2),则设z=
. |
| OM |
. |
| ON |
则y=-x+z+2,
∵|
. |
| MN |
| (x-2)2+(y-2)2 |
即(x-2)2+(y-2)2≤1,
平移直线y=-x+z+2,
由图象可知当直线经过点C(2,2)时,直线y=-x+z+2的截距最大,此时z=2-2+2=2,
当直线y=-x+z+2与圆相切时(圆下方),直线y=-x+z+2的截距最小,此时z最小.
直线一般式方程为x+y-2-z=0,
则圆心C到直线x+y-2-z=0的距离d=
| |2+2-2-z| | ||
|
| |z-2| | ||
|
解得z=2-
| 2 |
| 2 |
∵M、N是不同的两点,所以z无最大值,
∴2-
| 2 |
即
. |
| OM |
. |
| ON |
| 2 |
故选B.
点评:本题主要考查平面向量的数量积的运算,将正方体放入坐标系中,利用|
|≤1,建立M,N的轨迹方程,利用线性规划的知识解决数量积的取值范围,本题综合性较强,难度较大.
. |
| MN |

练习册系列答案
相关题目
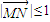 ,则
,则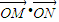 的取值范围是 .
的取值范围是 .