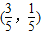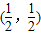题目内容
在集合A={（x，y）|0≤x≤5，0≤y≤5}内任取一个元素，则满足不等式x+y-4≥0的概率是分析：画出集合A中元素所表示的平面区域并求出其面积，求出满足不等式x+y-4≥0的平面区域并求出其面积，代入几何概型概率公式，即可得到答案．
解答：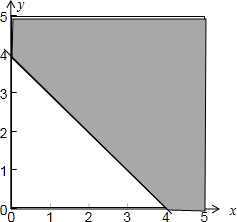
解：集合A={（x，y）|0≤x≤5，0≤y≤5}所表示的平面区域如下图中的正方形所示：
满足不等式x+y-4≥0的平面区域如下图中阴影部分所示：
∵S矩形=5×5=25，S阴影=25-
×4×4=17
故满足不等式x+y-4≥0的概率P=
故答案为：
解：集合A={（x，y）|0≤x≤5，0≤y≤5}所表示的平面区域如下图中的正方形所示：满足不等式x+y-4≥0的平面区域如下图中阴影部分所示：
∵S矩形=5×5=25，S阴影=25-
| 1 |
| 2 |
故满足不等式x+y-4≥0的概率P=
| 17 |
| 25 |
故答案为：
| 17 |
| 25 |
点评：本题考查的知识点是简单线性规划的应用，几何概型，其中求出基本事件总数和满足条件的基本事件数对应的平面区域的面积是解答本题的关键．
练习册系列答案
相关题目
设集合A=B={（x，y）|x∈R，y∈R}，从A到B的映射f：（x，y）→（x+2y，2x-y），则在映射f下B中的元素（1，1）对应的A中元素为（ ）
| A、（1，3） | ||||
| B、（1，1） | ||||
C、(
| ||||
D、(
|
