题目内容
已知二次函数 中
中 均为实数,且满足
均为实数,且满足 ,对于任意实数
,对于任意实数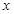 都有
都有 ,并且当
,并且当 时有
时有 成立。
成立。
(1)求 的值;
的值;
(2)证明: ;
;
(3)当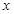 ∈[-2,2]且
∈[-2,2]且 取最小值时,函数
取最小值时,函数 (
( 为实数)是单调函数,求证:
为实数)是单调函数,求证: 。
。
【答案】
(Ⅰ)f(1)=1.(Ⅱ)略 (Ⅲ)略
【解析】本试题主要是考查了二次函数的解析式以及二次函数的最小值,以及二次不等式的综合运用。
(1)根据x≤f (x)≤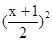 ,令x=1,得到1≤f (1)≤
,令x=1,得到1≤f (1)≤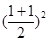 进而确定f(1)的值.(2)由a-b+c=0及f (1)=1得b=a+c=
进而确定f(1)的值.(2)由a-b+c=0及f (1)=1得b=a+c=  ,则f(x)-x≥0,即ax2-
,则f(x)-x≥0,即ax2-
x+c≥0,只需满足a>0且△≤0.从而得出ac≥ 
(3)a+c取得最小值时,a=c= 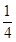 ,,F(x)=f(x)-mx=
,,F(x)=f(x)-mx= 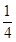 [x2+(2-4m)x+1].由f(x)是单调的,F(x)的顶点一定在[-2,2]的外边.推出
[x2+(2-4m)x+1].由f(x)是单调的,F(x)的顶点一定在[-2,2]的外边.推出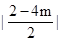 ≥2,解得m的范围即可
≥2,解得m的范围即可

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
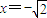 ,截x轴上的弦长为4,且过点(0,-1),求函数的解析式.
,截x轴上的弦长为4,且过点(0,-1),求函数的解析式. 的定义域为
的定义域为 ,若对于任意
,若对于任意 ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的取值范围是
.(用区间表示)
的取值范围是
.(用区间表示)