题目内容
已知二次函数的对称轴为x=-| 2 |
分析:由已知对称轴,则设二次函数的顶点式,再由截x轴上的弦长为4,可知与x轴的交点,最后由过点(0,-1)建立方程,求解即可.
解答:解:∵二次函数的对称轴为x=-
,
设所求函数为f(x)=a(x+
)2+b,
又∵f(x)截x轴上的弦长为4,
∴f(x)过点(-
+2,0),f(x)又过点(0,-1),
∴
,
,
∴f(x)=
(x+
)2-2.
函数的解析式:f(x)=
(x+
)2-2
| 2 |
设所求函数为f(x)=a(x+
| 2 |
又∵f(x)截x轴上的弦长为4,
∴f(x)过点(-
| 2 |
∴
|
|
∴f(x)=
| 1 |
| 2 |
| 2 |
函数的解析式:f(x)=
| 1 |
| 2 |
| 2 |
点评:本题主要考查二次函数设法,二次函数有三种形式,一是一般式,二是顶点式,三是根式形式,要根据条件灵活选择.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
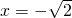 ,截x轴上的弦长为4,且过点(0,-1),求函数的解析式.
,截x轴上的弦长为4,且过点(0,-1),求函数的解析式.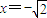 ,截x轴上的弦长为4,且过点(0,-1),求函数的解析式.
,截x轴上的弦长为4,且过点(0,-1),求函数的解析式.