题目内容
在平面直角坐标系中O为坐标原点,P(3,4),将向量
绕原点顺时针方向旋转
,并将其长度伸长为原来的2倍的向量
,则点Q的坐标是( )
| OP |
| π |
| 3 |
| OQ |
分析:先由复数的乘法法则计算出向量
所对应的复数,再由复数的几何意义即可得出点Q的坐标.
| OQ |
解答:解:由题意可知向量
所对应的复数=(3+4i)×2(cos(-
)+isin(-
))=(3+4i)(1-
i)=(3+4
)+(4-3
)i.
由复数的几何意义可知:点Q的坐标是(3+4
,4-3
).
故选A.
| OQ |
| π |
| 3 |
| π |
| 3 |
| 3 |
| 3 |
| 3 |
由复数的几何意义可知:点Q的坐标是(3+4
| 3 |
| 3 |
故选A.
点评:正确使用复数的乘法法则和理解复数的几何意义是解题的关键.

练习册系列答案
相关题目
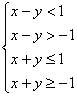 ,则点P的轨迹表示的平面区域为( )
,则点P的轨迹表示的平面区域为( )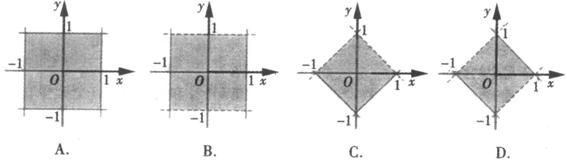
 绕原点顺时针方向旋转
绕原点顺时针方向旋转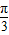 ,并将其长度伸长为原来的2倍的向量
,并将其长度伸长为原来的2倍的向量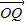 ,则点Q的坐标是( )
,则点Q的坐标是( )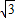 ,4-3
,4-3 )
)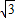 ,4-3
,4-3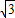 )
)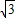 ,3
,3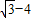 )
)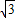 ,3-4
,3-4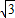 )
)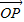 绕原点顺时针方向旋转
绕原点顺时针方向旋转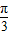 ,并将其长度伸长为原来的2倍的向量
,并将其长度伸长为原来的2倍的向量 ,则点Q的坐标是( )
,则点Q的坐标是( )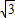 ,4-3
,4-3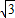 )
)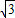 ,4-3
,4-3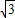 )
)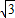 ,3
,3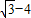 )
)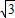 ,3-4
,3-4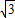 )
)