题目内容
已知倾斜角为45°的直线l过点A(1,-2)和点B,B在第一象限,|AB|=3| 2 |
(1)求点B的坐标;
(2)若直线l与双曲线C:
| x2 |
| a2 |
(3)对于平面上任一点P,当点Q在线段AB上运动时,称|PQ|的最小值为P与线段AB的距离.已知点P在x轴上运动,写出点P(t,0)到线段AB的距离h关于t的函数关系式.
分析:(1)先设直线AB方程为y=x-3,设点B(x,y),由
及B在第一象限求解.
(2)先联立直线方程与双曲线方程,消元转化为:(
-1)x2+6x-10=0,再由韦达定理求解.
(3)先设线段AB上任意一点Q坐标为Q(x,x-3),根据两点间的距离公式建立二次函数模型,|PQ|=
,
记f(x)=
=
(1≤t≤4),再根据对称轴和区间的相对位置,分类讨论求解.
|
(2)先联立直线方程与双曲线方程,消元转化为:(
| 1 |
| a2 |
(3)先设线段AB上任意一点Q坐标为Q(x,x-3),根据两点间的距离公式建立二次函数模型,|PQ|=
| (t-x)2+(x-3)2 |
记f(x)=
| (t-x)2+(x-3)2 |
2(x-
|
解答: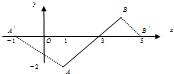 解:(1)直线AB方程为y=x-3,设点B(x,y),
解:(1)直线AB方程为y=x-3,设点B(x,y),
由
及x>0,y>0得x=4,y=1,点B的坐标为(4,1).
(2)由
得(
-1)x2+6x-10=0,
设E(x1,y1),F(x2,y2),则x1+x2=-
=4,得a=2.
(3)设线段AB上任意一点Q坐标为Q(x,x-3),|PQ|=
,
记f(x)=
=
(1≤t≤4),
当1≤
≤4时,即-1≤t≤5时,|PQ|min=f(
)=
,
当
>4,即t>5时,f(x)在[1,4]上单调递减,|PQ|min=f(4)=
;
当
<1,即t<-1时,f(x)在[1,4]上单调递增,|PQ|min=f(1)=
.
综上所述,h(t)=
 解:(1)直线AB方程为y=x-3,设点B(x,y),
解:(1)直线AB方程为y=x-3,设点B(x,y),由
|
(2)由
|
| 1 |
| a2 |
设E(x1,y1),F(x2,y2),则x1+x2=-
| 6a2 |
| 1-a2 |
(3)设线段AB上任意一点Q坐标为Q(x,x-3),|PQ|=
| (t-x)2+(x-3)2 |
记f(x)=
| (t-x)2+(x-3)2 |
2(x-
|
当1≤
| t+3 |
| 2 |
| t+3 |
| 2 |
| |t-3| | ||
|
当
| t+3 |
| 2 |
| (t-4)2+1 |
当
| t+3 |
| 2 |
| (t-1)2+4 |
综上所述,h(t)=
|
点评:本题主要考查直线与圆的位置关系,中点坐标公式及两点间的距离公式,同时考查了建立函数模型求最值的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知倾斜角为45°的直线经过A(2,4),B(1,m)两点,则m=( )
| A、3 | B、-3 | C、5 | D、-1 |