题目内容
有下列各式: ,
, ,
, ,……
,……
则按此规律可猜想此类不等式的一般形式为: .
 ,
, ,
, ,……
,……则按此规律可猜想此类不等式的一般形式为: .
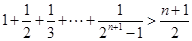 (
(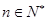 )
)试题分析:观察给定的式子左边和式的分母是从1,2,3,……,直到
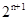 ,右边分母为2,分子为n+1,故猜想此类不等式的一般形式为:
,右边分母为2,分子为n+1,故猜想此类不等式的一般形式为: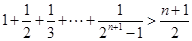 (
(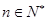 )。
)。点评:简单题,归纳推理,就是从个别性知识推出一般性结论的推理。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
 ,
, ,
, ,……
,……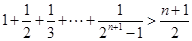 (
(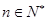 )
)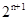 ,右边分母为2,分子为n+1,故猜想此类不等式的一般形式为:
,右边分母为2,分子为n+1,故猜想此类不等式的一般形式为: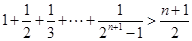 (
(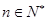 )。
)。
 阅读快车系列答案
阅读快车系列答案