题目内容

已知函数f(x)的定义域是（0，+∞），当x>1时，f(x)>0，且f(x·y)＝f(x)+f(y)，

(1)求f(1)的值；

(2)证明f(x)在定义域上是增函数；

(3)如果f( 3 )=1，求满足不等式f(x)－f()≥2的x的取值范围．

解：（1）令x=y=1，得f(1)=2f(1)，故f(1)=0. ………………………………2分

(2)令y= ,得f(1)=f(x)+f()=0,故f()=－f(x). ………………………………4分

任取x1,x2∈（0，+∞）,且x1<x2,则f(x2)－f(x1)=f(x2)+f()=f().…………………6分

由于>1，故f()>0，从而f(x1)>f(x2).  ∴f(x)在（0，+∞）上是增函数. …………8分

(3)由于f(3)=1，在f(x·y)＝f(x)+f(y)中，令x=y=3，得f(9)=f(3)+f(3)=2。……10分

又－f()=f(x－2)，故所给不等式可化为f(x)+f(x－2) ≥f(9)，即 f [x(x－2)] ≥f(9)，

解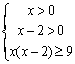得.∴x的取值范围是.…………………14分

练习册系列答案
相关题目
已知函数f(x)=
1
3
x3+
a-3
2
x2+(a2-3a)x-2a．
（I）如果对任意x∈[1，2]，f′（x）＞a2恒成立，求实数a的取值范围；
（II）设函数f（x）的两个极值点分别为x1，x2判断下列三个代数式：①x1+x2+a，②
x
2
1
+
x
2
2
+a2，③
x
3
1
+
x
3
2
+a3
中有几个为定值？并且是定值请求出；若不是定值，请把不是定值的表示为函数g（a），并求出g（a）的最小值．
问题1：已知函数f(x)=
x
1+x
，则f(
1
10
)+f(
1
9
)+…+f(
1
2
)+f(1)+f(2)+…+f（9）+f（10）=
19
2
19
2
．
我们若把每一个函数值计算出，再求和，对函数值个数较少时是常用方法，但函数值个数较多时，运算就较繁锁．观察和式，我们发现f(
1
2
)+f(2)、…、f(
1
9
)+f(9)、f(
1
10
)+f(10)可一般表示为f(
1
x
)+f(x)=
1
x
1+
1
x
+
x
1+x
=
1
1+x
+
x
1+x
=
1+x
1+x
=1为定值，有此规律从而很方便求和，请求出上述结果，并用此方法求解下面问题：
问题2：已知函数f(x)=
1
2x+
2
，求f（-2007）+f（-2006）+…+f（-1）+f（0）+f（1）+…+f（2007）+f（2008）的值．
已知函数f(x)=log3
3
x
1-x
，M(x1，y1)，N(x2，y2)是f（x）图象上的两点，横坐标为
1
2
的点P是M，N的中点．
（1）求证：y1+y2为定值；
（2）若Sn=f(
1
n
)+f(
2
n
)+…+f(
n-1
n
)（n∈N*，n≥2），求
lim
n→∞
4Sn-9Sn
4Sn+1+9Sn+1
的值；
（3）在（2）的条件下，若an=
1
6
，n=1
1
4(Sn+1)(Sn+1+1)
，n≥2
（n∈N*），Tn为数列{an}的前n项和，若Tn＜m（Sn+1+1）对一切n∈N*都成立，试求实数m的取值范围．
已知函数f(x)=
x+1-a
a-x
(x≠a)
（1）当f（x）的定义域为[a+
1
2
，a+1]时，求f（x）的值域；
（2）试问对定义域内的任意x，f（2a-x）+f（x）的值是否为一个定值？若是，求出这个定值；若不是，说明理由；
（3）设函数g（x）=x2+|（x-a）f（x）|，若
1
2
≤a≤
3
2
，求g（x）的最小值．
（2009•嘉定区一模）（理）已知函数f(x)=log2
2
x
1-x
，P1（x1，y1）、P2（x2，y2）是f（x）图象上两点．
（1）若x1+x2=1，求证：y1+y2为定值；
（2）设Tn=f(
1
n
)+f(
2
n
)+…+f(
n-1
n
)，其中n∈N*且n≥2，求Tn关于n的解析式；
（3）对（2）中的Tn，设数列{an}满足a1=2，当n≥2时，an=4Tn+2，问是否存在角a，使不等式(1-
1
a1
)(1-
1
a2
)…(1-
1
an
)＜
sinα
2n+1
对一切n∈N*都成立？若存在，求出角α的取值范围；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网