题目内容
已知动圆过定点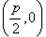 ,且与直线
,且与直线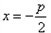 相切,其中p>0,
相切,其中p>0,
(Ⅰ)求动圆圆心C的轨迹的方程;
(Ⅱ)设A、B是轨迹C上异于原点O的两个不同点,直线OA和OB的倾斜角分别为α和β,当α,β变化且α+β为定值θ(0<θ<π)时,证明直线AB恒过定点,并求出该定点的坐标。
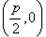 ,且与直线
,且与直线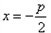 相切,其中p>0,
相切,其中p>0,(Ⅰ)求动圆圆心C的轨迹的方程;
(Ⅱ)设A、B是轨迹C上异于原点O的两个不同点,直线OA和OB的倾斜角分别为α和β,当α,β变化且α+β为定值θ(0<θ<π)时,证明直线AB恒过定点,并求出该定点的坐标。
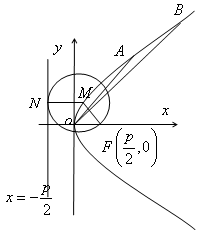
解:(Ⅰ)如图,设M为动圆圆心,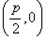 为记为F,
为记为F,
过点M作直线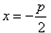 的垂线,垂足为N,
的垂线,垂足为N,
由题意知:|MF|=|MN|,即动点M到定点F与定直线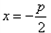 的距离相等,
的距离相等,
由抛物线的定义知,点M的轨迹为抛物线,其中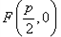 为焦点,
为焦点,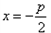 为准线,
为准线,
所以轨迹方程为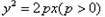 ;
;
(Ⅱ)如图,设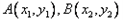 ,
,
由题意得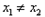 (否则
(否则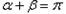 )且
)且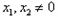 ,
,
所以直线AB的斜率存在,设其方程为y=kx+b,
显然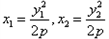 ,
,
将y=kx+b与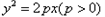 联立消去x,得
联立消去x,得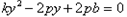 ,
,
由韦达定理知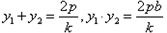 ,①
,①
(1)当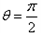 时,即
时,即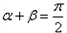 时,
时,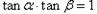 ,
,
所以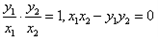 ,
,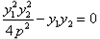 ,
,
所以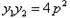 ,
,
由①知: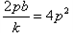 ,所以b=2pk,
,所以b=2pk,
因此直线AB的方程可表示为y=kx+2pk,即k(x+2p)-y=0,
所以直线AB恒过定点(-2p,0);
(2)当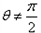 时,由
时,由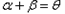 ,
,
得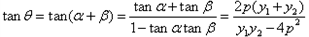 ,
,
将①式代入上式整理化简可得: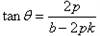 ,
,
所以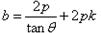 ,
,
此时,直线AB的方程可表示为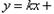
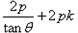 ,
,
即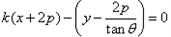 ,
,
所以直线AB恒过定点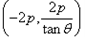 ;
;
所以由(1)(2)知,当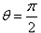 时,直线AB恒过定点(-2p,0);
时,直线AB恒过定点(-2p,0);
当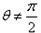 时直线AB恒过定点
时直线AB恒过定点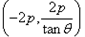 。
。
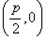 为记为F,
为记为F,过点M作直线
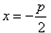 的垂线,垂足为N,
的垂线,垂足为N,由题意知:|MF|=|MN|,即动点M到定点F与定直线
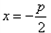 的距离相等,
的距离相等,由抛物线的定义知,点M的轨迹为抛物线,其中
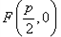 为焦点,
为焦点,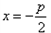 为准线,
为准线,所以轨迹方程为
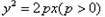 ;
;(Ⅱ)如图,设
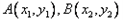 ,
,由题意得
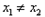 (否则
(否则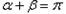 )且
)且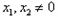 ,
,所以直线AB的斜率存在,设其方程为y=kx+b,
显然
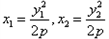 ,
,将y=kx+b与
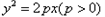 联立消去x,得
联立消去x,得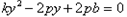 ,
,由韦达定理知
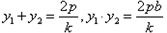 ,①
,①(1)当
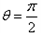 时,即
时,即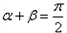 时,
时,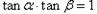 ,
,所以
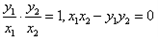 ,
,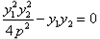 ,
,所以
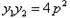 ,
,由①知:
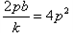 ,所以b=2pk,
,所以b=2pk,因此直线AB的方程可表示为y=kx+2pk,即k(x+2p)-y=0,
所以直线AB恒过定点(-2p,0);
(2)当
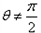 时,由
时,由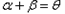 ,
,得
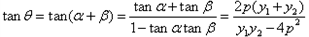 ,
,将①式代入上式整理化简可得:
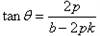 ,
,所以
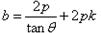 ,
,此时,直线AB的方程可表示为
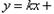
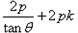 ,
,即
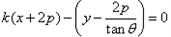 ,
,所以直线AB恒过定点
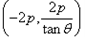 ;
;所以由(1)(2)知,当
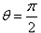 时,直线AB恒过定点(-2p,0);
时,直线AB恒过定点(-2p,0);当
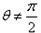 时直线AB恒过定点
时直线AB恒过定点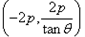 。
。
练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 (1) 求动圆的圆心轨迹
(1) 求动圆的圆心轨迹 过定点
过定点 ,且与直线
,且与直线 相切,椭圆
相切,椭圆 的对称轴为坐标轴,一个焦点是
的对称轴为坐标轴,一个焦点是 ,点
,点 在椭圆
在椭圆 的方程及其椭圆
的方程及其椭圆 与轨迹
与轨迹 处的切线平行,且直线
处的切线平行,且直线 两点,问:是否存在着这样的直线
两点,问:是否存在着这样的直线 的面积等于
的面积等于 ?如果存在,请求出直线
?如果存在,请求出直线