题目内容
设编号为1,2,3,4,5,6的六个茶杯与编号为1,2,3,4,5,6的六个茶杯盖,将这六个杯盖盖在茶杯上,恰好有2 个杯盖与茶杯编号相同的盖法有
| A.24种 | B.135种 | C.9种 | D.360种 |
B
解析试题分析:首先从6个号中选两个放到同号的盒子里,共有C62种结果,剩下的四个小球和四个盒子,要求球的号码与盒子的号码不同,首先第一个球有3种结果,与被放上球的盒子同号的球有三种方法,余下的只有一种方法,根据分步计数原理的结果解:由题意知本题是一个分步计数问题,首先从6个号中选两个放到同号的盒子里,共有C62=15种结果,剩下的四个小球和四个盒子,要求球的号码与盒子的号码不同,首先第一个球有3种结果,与被放上球的盒子同号的球有三种方法,余下的只有一种方法共有3×3=9种结果,根据分步计数原理得到共有15×9=135种结果.故选B.
考点:分步计数问题
点评:本题考查分步计数问题,本题解题的关键是选出球号和盒子号一致的以后4个小球和四个盒子的方法,本题是一个基础题

练习册系列答案
相关题目
某大学的8名同学准备拼车去旅游,其中大一、大二、大三、大四每个年级各两名,分乘甲、乙两辆汽车.每车限坐4名同学(乘同一辆车的4名同学不考虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的4名同学中恰有2名同学是来自于同一年级的乘坐方式共有
| A.24种 | B.18种 | C.48种 | D.36种 |
从5双不同的手套中任取4只,恰有两只是同一双的概率为( )
A.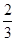 | B.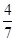 | C.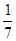 | D.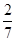 |
(1+2x) 6的展开式中,x的系数等于 ,则函数
,则函数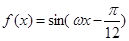 的最小正周期是
的最小正周期是
A. | B. | C. | D. |
从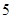 位男数学教师和
位男数学教师和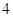 位女数学教师中选出
位女数学教师中选出 位教师派到
位教师派到 个班担任班主任(每班
个班担任班主任(每班 位班主任),要求这
位班主任),要求这 位班主任中男女教师都有,则不同的选派方案共有( )
位班主任中男女教师都有,则不同的选派方案共有( )
| A.210 | B.420 | C.630 | D.840 |
在 展开式中,
展开式中, 的系数为( ).
的系数为( ).
| A.360 | B.180 | C.﹣360 | D.-180 |
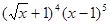 的展开式中,
的展开式中,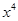 的系数为( )
的系数为( )
| A.-40 | B.10 | C.40 | D.45 |
 的展开式中
的展开式中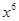 的系数是( )
的系数是( )
A. | B. | C. | D. |
 的值由右上面程序框图算出,则二项式
的值由右上面程序框图算出,则二项式 展开式的常数项为 ( )
展开式的常数项为 ( )



