题目内容
给出问题:设F1、F2是双曲线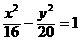 的焦点,点P是双曲线上的动点,点P到焦点F1的距离等于9,求点P到F2的距离,某同学的解答如下:双曲线的实轴长为8,由|PF1-PF2|=8即|9-PF2|=8,得PF2=1或PF2= 17.试问该同学的解答是否正确?若正确,请说明依据;若不正确,请说明理由.
的焦点,点P是双曲线上的动点,点P到焦点F1的距离等于9,求点P到F2的距离,某同学的解答如下:双曲线的实轴长为8,由|PF1-PF2|=8即|9-PF2|=8,得PF2=1或PF2= 17.试问该同学的解答是否正确?若正确,请说明依据;若不正确,请说明理由.
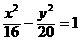 的焦点,点P是双曲线上的动点,点P到焦点F1的距离等于9,求点P到F2的距离,某同学的解答如下:双曲线的实轴长为8,由|PF1-PF2|=8即|9-PF2|=8,得PF2=1或PF2= 17.试问该同学的解答是否正确?若正确,请说明依据;若不正确,请说明理由.
的焦点,点P是双曲线上的动点,点P到焦点F1的距离等于9,求点P到F2的距离,某同学的解答如下:双曲线的实轴长为8,由|PF1-PF2|=8即|9-PF2|=8,得PF2=1或PF2= 17.试问该同学的解答是否正确?若正确,请说明依据;若不正确,请说明理由.解:该同学的解答不正确.
理由如下:由定义|PF1-PF2|=8 ,双曲线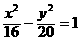 中,
中,
c=6,F1F2=12,
∴PF1+PF2≥12,
当P,F1,F2在同一直线上时取得“=”,
由|PF1-PF2|=8得PF1-PF2=±8,
P在双曲线的左右支上时,PF1≥2或PF1≥10,
同理,PF2≥2或PF2≥10,
因此,PF2根本不可能为1,而只能为17.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 的两个焦点,点F1、F2到直线L:
的两个焦点,点F1、F2到直线L: x-y+
x-y+ =0的距离分别为d1、d2,试求d1•d2的值,并判断直线L与椭圆M的位置关系.
=0的距离分别为d1、d2,试求d1•d2的值,并判断直线L与椭圆M的位置关系. (a>b>0)的两个焦点,点F1、F2到直线L:mx+ny+p=0(m、n不同时为0)的距离分别为d1、d2,且直线L与椭圆M相切,试求d1•d2的值.
(a>b>0)的两个焦点,点F1、F2到直线L:mx+ny+p=0(m、n不同时为0)的距离分别为d1、d2,且直线L与椭圆M相切,试求d1•d2的值.