题目内容
若曲线的极坐标方程为ρ=2sinθ+4cosθ，以极点为原点，极轴为x轴正半轴建立直角坐标系，则该曲线的直角坐标方程为
（x-2）2+（y-1）2=5
（x-2）2+（y-1）2=5
．分析：曲线方程即 ρ2=2ρsinθ+4ρcosθ，化为直角坐标方程并化简为 （x-2）2+（y-1）2=5，由此得到答案．
解答：解：曲线的极坐标方程为ρ=2sinθ+4cosθ，即 ρ2=2ρsinθ+4ρcosθ，
即x2+y2=2y+4x，化简为 （x-2）2+（y-1）2=5，
故答案为 （x-2）2+（y-1）2=5．
即x2+y2=2y+4x，化简为 （x-2）2+（y-1）2=5，
故答案为 （x-2）2+（y-1）2=5．
点评：本题主要考查把极坐标方程化为直角坐标方程的方法，利用了公式x=ρcosθ，y=ρsinθ，属于基础题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
，以极点为原点，极轴为
轴正半轴建立直角坐标系，则该曲线的直角坐标方程为 .
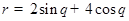，以极点为原点，极轴为
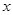轴正半轴建立直角坐标系，则该曲线的直角坐标方程为