题目内容
甲、乙两人做掷骰子游戏,两人各掷一次,谁掷得的点数多谁就取胜,求甲取胜的概率.
【探究】首先列举出所有可能的基本事件,列出所求事件包含的基本事件,再根据古典概型的概率公式进行计算.
【解法一】甲将骰子抛掷一次,出现的点数有1、2、3、4、5、6这6种结果,对甲掷得的每个结果,乙又掷得点数分别为1、2、3、4、5、6这6种结果,于是共有6×6=36种不同的结果.
把甲掷得i点,乙掷得j点(1≤i,j≤6)记为(i,j).
事件“甲取胜”包含下列15种结果:
(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),(6,1),(6,2),(6,3),(6,4),(6,5).
故甲取胜的概率为![]() =
=![]() .
.
【解法二】两从掷出相同的点数有(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)六种结果,“甲掷得的点数比乙多”与“乙掷得的点数比甲多”是等可能性事件,都有![]() =15种结果.故甲取胜的概率为
=15种结果.故甲取胜的概率为![]() =
=![]() .
.
规律总结 掷骰子是典型的题型,本题与解析几何知识相联系,在如图3-2-2所示的直角坐标系中,若x表示甲掷得的点数,y表示乙掷得的点数,本题实质就是求点(x,y)落在直线y=x下方的概率.
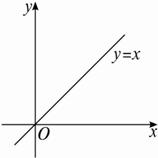
图3-2-2

练习册系列答案
相关题目