题目内容
已知函数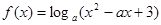
(1)若函数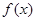 的值域为
的值域为 ,求实数
,求实数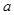 的取值范围;
的取值范围;
(2)当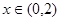 时,函数
时,函数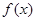 恒有意义,求实数
恒有意义,求实数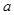 的取值范围.
的取值范围.
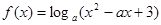
(1)若函数
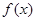 的值域为
的值域为 ,求实数
,求实数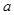 的取值范围;
的取值范围;(2)当
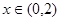 时,函数
时,函数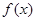 恒有意义,求实数
恒有意义,求实数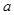 的取值范围.
的取值范围.(1) ;(2)
;(2)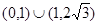 .
.
 ;(2)
;(2)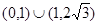 .
.试题分析:(1)对数函数的值域为
 ,意味着真数可以取遍一切正实数,故内层二次函数应与
,意味着真数可以取遍一切正实数,故内层二次函数应与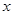 轴有交点,即
轴有交点,即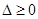 ,解得
,解得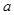 的范围;
的范围;(2)函数
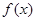 恒有意义,即真数大于零恒成立,利用参变分离法解决此恒成立问题即可得
恒有意义,即真数大于零恒成立,利用参变分离法解决此恒成立问题即可得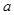 的取值范围
的取值范围试题解析:(1)令
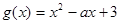 ,由题设知
,由题设知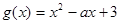 需取遍
需取遍 内任意值,
内任意值,所以
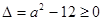 解得
解得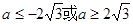
故
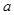 的取值范围为
的取值范围为 .
.(2)
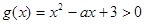 对一切
对一切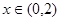 恒成立且
恒成立且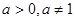
即
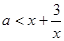 对一切
对一切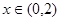 恒成立
恒成立令
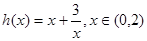 ,当
,当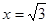 时,
时,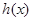 取得最小值为
取得最小值为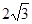 ,
,得:
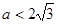
又因为:
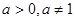
所以:
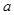 的取值范围为
的取值范围为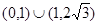 .
.
练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
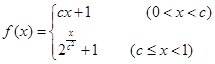 ,且
,且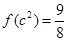 .
.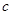 的值;
的值;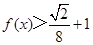 .
.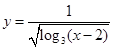 的定义域为( )
的定义域为( )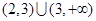 ;
;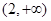 ;
;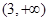 ;
;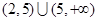 ;
;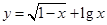 的定义域为 .
的定义域为 .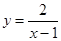 的定义域是
的定义域是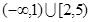 ,则其值域为( )
,则其值域为( )
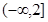

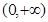
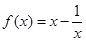 ,则( )
,则( )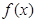 的定义域为
的定义域为 ,值域为
,值域为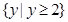
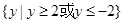
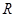
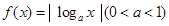 的定义域为
的定义域为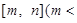
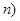 ,值域为
,值域为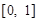 ,若
,若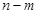 的最小值为
的最小值为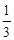 ,则实数
,则实数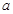 的值为( )
的值为( )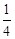
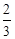
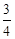
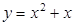
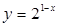
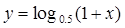
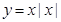
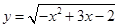 的定义域是 .
的定义域是 .