题目内容
(本小题满分12分)
已知p:方程x2+mx+1=0有两个不相等的负实根;q:不等式4x2+4(m-2)x+1>0的解集为R,若p或q为真命题,p且q为假命题,求m的取值范围.
已知p:方程x2+mx+1=0有两个不相等的负实根;q:不等式4x2+4(m-2)x+1>0的解集为R,若p或q为真命题,p且q为假命题,求m的取值范围.
解:

q为真命题?△=[4(m-2)]2-4×4×1<0⇒1<m<3. ------------8分
∵p或q为真,p且q为假,∴p与q一真一假.
若p真q假,则m>2,且m≤1或m≥3,所以m≥3.
若p假q真,则m≤2,且1<m<3,所以1<m≤2.
综上所述,m的取值范围为{m|1<m≤2,或m≥3}. -----------12分

q为真命题?△=[4(m-2)]2-4×4×1<0⇒1<m<3. ------------8分
∵p或q为真,p且q为假,∴p与q一真一假.
若p真q假,则m>2,且m≤1或m≥3,所以m≥3.
若p假q真,则m≤2,且1<m<3,所以1<m≤2.
综上所述,m的取值范围为{m|1<m≤2,或m≥3}. -----------12分
略

练习册系列答案
相关题目
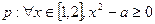 ,命题
,命题
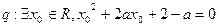 ,
,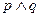 是真命题,求实数a的取值范围.
是真命题,求实数a的取值范围.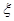 服从正态分布
服从正态分布 ,
, ,且
,且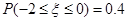 ,则
,则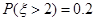
 ,当变量
,当变量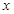 增加一个单位时,
增加一个单位时,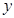 平均增加
平均增加 个单位;
个单位;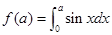 ,则
,则 ;
; :
: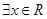 ,使得
,使得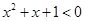 ,则
,则 :
: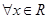 ,均有
,均有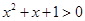
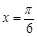 ”是“
”是“ ”的充分不必要条件; ②若“
”的充分不必要条件; ②若“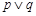 ”为真,则“
”为真,则“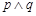 ”为真; ③命题
”为真; ③命题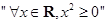 的否定是
的否定是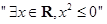 ;
; 的绝对值越接近于
的绝对值越接近于 ,表明两个随机变量线性相关性越强;
,表明两个随机变量线性相关性越强; ,
, ,
,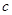
 ,且
,且 ,则下列命题正确的是( )
,则下列命题正确的是( ) ,则
,则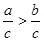
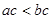 ,则
,则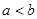

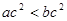 ,则
,则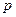 是真命题,
是真命题,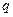 是假命题,则
是假命题,则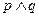 是真命题
是真命题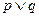 是假命题
是假命题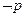 是真命题
是真命题 是真命题
是真命题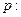 方程
方程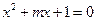 有两个不等的负根;
有两个不等的负根;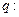 方程
方程 无实根,若
无实根,若 或
或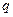 为真,
为真,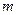 的取值范围。
的取值范围。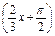 是奇函数;
是奇函数;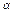 ,使得sin
,使得sin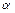 +cos
+cos ;
;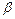 是第一象限角且
是第一象限角且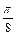 是函数y=sin
是函数y=sin 的一条对称轴方程;
的一条对称轴方程;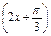 的图象关于点
的图象关于点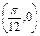 成中心对称图形.
成中心对称图形. 、
、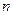 是两条不同的直线,
是两条不同的直线,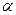 、
、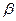 、
、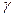 是三个不同的平面,给出下列四个命题:①若
是三个不同的平面,给出下列四个命题:①若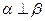 ,
,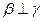 ,则
,则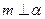 ,则
,则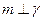 ;
;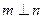 .其中正确命题的序号是 .
.其中正确命题的序号是 .