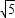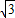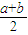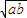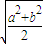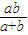题目内容
若实数m，n，x，y满足m2+n2=a，x2+y2=b，则mx+ny的最大值（ ）A．
B．
C．
D．
【答案】分析：可利用三角换元求解．令m=
cosα，n=
sinα，x=
cosβ，y=
sinβ，将其代入mx+ny中，由三角函数公式分析可得答案．
解答：解：令m=
cosα，n=
sinα，x=
cosβ，y=
sinβ，
则mx+ny=
cosαcosβ+
sinαsinβ=
cos（α-β）≤
故选B
点评：本题主要考查求最值问题，容易误选A，主要是对利用基本不等式求最值的条件忽略．
cosα，n=sinα，x=cosβ，y=sinβ，将其代入mx+ny中，由三角函数公式分析可得答案．解答：解：令m=
cosα，n=sinα，x=cosβ，y=sinβ，则mx+ny=
cosαcosβ+sinαsinβ=cos（α-β）≤故选B
点评：本题主要考查求最值问题，容易误选A，主要是对利用基本不等式求最值的条件忽略．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
若实数m，n，x，y满足m2+n2=a，x2+y2=b，则mx+ny的最大值（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
