题目内容
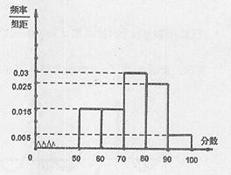
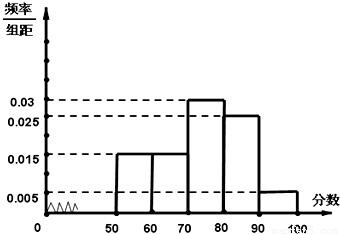
 某校从参加高三年级期末考试的280名文科学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如右部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高三年级期末考试的280名文科学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如右部分频率分布直方图.观察图形的信息,回答下列问题:(1)补全这个频率分布直方图;若达60分为极格,请估计这280名文科学生中的及格人数;
(2)用分层抽样的方法在分数段为[60,80)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[70,80)的概率.
【答案】分析:(1)频率分布直方图中,小矩形的面积等于这一组的频率,而频率的和等于1,可求出分数在[70,80)内的频率,即可求出矩形的高,画出图象即可;计算出60分以上的累积频率,可估算出这280名文科学生中的及格人数;
(2)根据分层抽样的抽样比,计算出分数段[70,80)的抽取人数,进而求出从样本中任取2人的所有基本事件个数及满足至多有1人在分数段[70,80)的基本事件个数,代入古典概型公式,可得答案.
解答: 解:(1)分数在[70,80)内的频率为:
解:(1)分数在[70,80)内的频率为:
1-(0.010+0.015+0.015+0.025+0.005)×10=1-0.7=0.3
故该组在频率分布直方图中对应矩形的高为
补全频率分布直方图如图所示:
及格的频率是(0.3+0.015+0.025+0.005)×10=0.75
故这280名文科学生中的及格人数约为280×0.75=210(人)
(2)由(1)得分数在[60,70)内的频数为0.015×60=9人,
分数在[70,80)内的频数为0.030×60=18人,
∵在分数段为[60,80)的学生中抽取一个容量为6的样本,
∴在分数段[60,70)中应抽取2人,分别记为(M,N);在分数段[70,80)中应抽取2人,分别记为(A,B,C,D)
记从样本中任取2人,至多有1人在分数段[70,80)为事件A
则基本事件总数有 =
= =15个,分别为:
=15个,分别为:
(M,N),(M,A),(M,B),(M,C),(M,D)
(N,A),(N,B),(N,C),(N,D),(A,B),
(A,C),(A,D),(B,C),(B,D),(C,D)
事件A包含的基本事件有: =2×4+1=9个,分别为
=2×4+1=9个,分别为
(M,N),(M,A),(M,B),(M,C),(M,D)
(N,A),(N,B),(N,C),(N,D)
故P(A)= =
=
点评:本题主要考查根据频率分布直方图求某种情况的频率和频数,考察了学生的识图能力和转化能力.
(2)根据分层抽样的抽样比,计算出分数段[70,80)的抽取人数,进而求出从样本中任取2人的所有基本事件个数及满足至多有1人在分数段[70,80)的基本事件个数,代入古典概型公式,可得答案.
解答:
 解:(1)分数在[70,80)内的频率为:
解:(1)分数在[70,80)内的频率为:1-(0.010+0.015+0.015+0.025+0.005)×10=1-0.7=0.3
故该组在频率分布直方图中对应矩形的高为

补全频率分布直方图如图所示:
及格的频率是(0.3+0.015+0.025+0.005)×10=0.75
故这280名文科学生中的及格人数约为280×0.75=210(人)
(2)由(1)得分数在[60,70)内的频数为0.015×60=9人,
分数在[70,80)内的频数为0.030×60=18人,
∵在分数段为[60,80)的学生中抽取一个容量为6的样本,
∴在分数段[60,70)中应抽取2人,分别记为(M,N);在分数段[70,80)中应抽取2人,分别记为(A,B,C,D)
记从样本中任取2人,至多有1人在分数段[70,80)为事件A
则基本事件总数有
 =
= =15个,分别为:
=15个,分别为:(M,N),(M,A),(M,B),(M,C),(M,D)
(N,A),(N,B),(N,C),(N,D),(A,B),
(A,C),(A,D),(B,C),(B,D),(C,D)
事件A包含的基本事件有:
 =2×4+1=9个,分别为
=2×4+1=9个,分别为(M,N),(M,A),(M,B),(M,C),(M,D)
(N,A),(N,B),(N,C),(N,D)
故P(A)=
 =
=
点评:本题主要考查根据频率分布直方图求某种情况的频率和频数,考察了学生的识图能力和转化能力.

练习册系列答案
相关题目
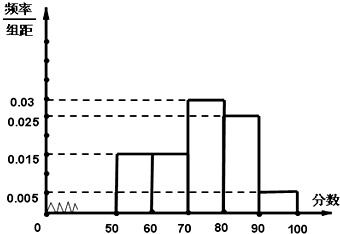 某校从参加高三年级期末考试的学生中抽出60名学生,并统计了他们的化学成绩(成绩均为整数且满分为100分),把其中不低于50分的成绩分成五段[50,60),[60,70)…[90,100]后,画出部分频率分布直方图(如图),那么化学成绩在[70,80)的学生人数为
某校从参加高三年级期末考试的学生中抽出60名学生,并统计了他们的化学成绩(成绩均为整数且满分为100分),把其中不低于50分的成绩分成五段[50,60),[60,70)…[90,100]后,画出部分频率分布直方图(如图),那么化学成绩在[70,80)的学生人数为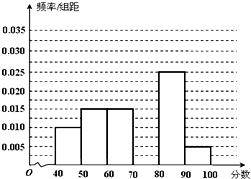 某校从参加高三年级期末考试的280名文科学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如右部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高三年级期末考试的280名文科学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如右部分频率分布直方图.观察图形的信息,回答下列问题: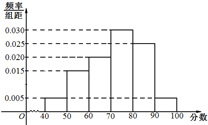 某校从参加高三年级期末统考测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
某校从参加高三年级期末统考测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示. 后,画出部分
后,画出部分 的学生人数为
。
的学生人数为
。