Question

如图2-2-17,ABCD—A′B′C′D′为长方体,底面是边长为a的正方形,高为2a,M,N分别是CD和AD的中点.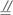

图2-2-17

(1)判断四边形MNA′C′的形状.

(2)求四边形MNA′C′的面积.

Answer 1

思路分析:可由MN∥AC,AC∥A′C′,得出MN∥A′C′,这是求解问题的关键所在.要注意挖掘长方体的隐含条件.

解:(1)连结AC.

因为M,N分别是CD和AD的中点,

所以MNAC.

因为ABCD—A′B′C′D′为长方体,

所以ACC′A′为矩形.所以A′C′AC.所以MNA′C′.

所以四边形MNA′C′是梯形.

在△A′AN和△C′CM中,因为∠A′AN=∠C′CM=90°,

A′A=C′C=2a,AN=CN=a.

所以△A′AN≌△C′CM.所以A′N=C′M.

所以四边形MNA′C′是等腰梯形.

(2)由A′C′=a,MN=a,A′N=C′M=a得,梯形高h=a,

所以S=a².

  绿色通道:抓住图形特征,将问题转化为具体的线面关系,把线面平行变为线线平行是处理空间几何问题常用的思想方法.