题目内容
如果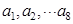 为各项都大于零的等差数列,公差
为各项都大于零的等差数列,公差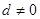 ,则
,则
A.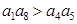 | B. |
C.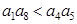 | D.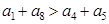 |
C
解析试题分析:∵1+8=4+5,∴a1+a8=a4+a5,∴排除D;
若令an=n,则a1a8=1•8<20=4•5=a4a5,∴排除A,B.
故选C.
考点:本题主要考查等差数列的通项公式,等差数列的性质。
点评:简单题,在等差数列中, 则
则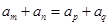 。本题通过特取数列an=n,利用“排除法”,使问题得解。
。本题通过特取数列an=n,利用“排除法”,使问题得解。

练习册系列答案
相关题目
已知数列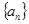 满足
满足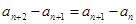 ,
,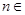 N*,且
N*,且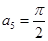 。若函数
。若函数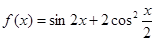 ,记
,记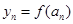 ,则
,则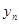 的前9项和为
的前9项和为
A. | B.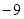 | C.9 | D.1 |
在等差数列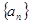 中,若
中,若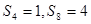 ,则
,则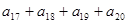 的值为( )
的值为( )
| A.9 | B.12 | C.16 | D.17 |
已知在等差数列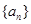 中,
中,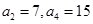 ,则前10项和
,则前10项和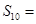 ( )
( )
| A.100 | B.210 | C.380 | D.400 |
数列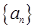 中,
中,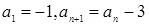 ,则
,则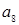 等于( )
等于( )
A.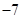 | B. | C.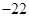 | D.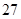 |
设等差数列 的前
的前 项和为
项和为 ,若
,若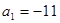 ,
,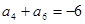 ,则当
,则当 取最小值时,
取最小值时, 等于( )
等于( )
| A.6 | B.7 | C.8 | D.9 |
由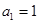 ,
,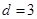 确定的等差数列
确定的等差数列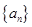 ,当
,当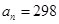 时,序号
时,序号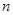 等于 ( )
等于 ( )
| A.99 | B.100 | C.96 | D.101 |
已知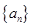 是等差数列,
是等差数列,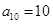 ,其前10项和
,其前10项和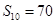 ,则其公差
,则其公差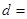 ( )
( )
A.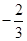 | B.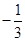 | C.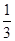 | D.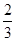 |
已知等差数列 中,
中,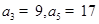 ,记数列
,记数列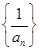 的前
的前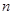 项和为
项和为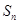 ,若
,若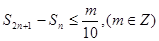 ,对任意的
,对任意的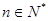 成立,则整数
成立,则整数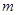 的最小值为
的最小值为
| A.5 | B.4 | C.3 | D.2 |