题目内容
若两等差数列{an}、{bn}前n项和分别为An、Bn,满足
=
(n∈N+),则
的值为( )
| An |
| Bn |
| 7n+1 |
| 4n+27 |
| a11 |
| b11 |
分析:题目给出了两个等差数列的前n项和的比,要求两等差数列的第11项的比,可根据第11项是前21项的中间项,把第11项的比转化为前21项和的比.
解答:解:∵数列{an}、{bn}是等差数列,且其前n项和分别为An、Bn,
由等差数列的性质得,A21=
=21a11,B21=
=21b11,
∵足
=
(n∈N+),
∴
=
=
=
=
.
故选:C.
由等差数列的性质得,A21=
| (a1+a21)×21 |
| 2 |
| (b1+b21)×21 |
| 2 |
∵足
| An |
| Bn |
| 7n+1 |
| 4n+27 |
∴
| a11 |
| b11 |
| 21a11 |
| 21b11 |
| A21 |
| B21 |
| 7×21+1 |
| 4×21+27 |
| 4 |
| 3 |
故选:C.
点评:本题考查了等差数列的性质,考查了等差数列的前n项和公式,体现数学转化思想方法,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
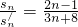 ,则
,则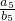 的值为________.
的值为________. ,则
,则 的值为 .
的值为 . ,则
,则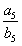 的值为( )。
的值为( )。