题目内容
设点 是曲线
是曲线 上的点,
上的点, ,则( )
,则( )
 是曲线
是曲线 上的点,
上的点, ,则( )
,则( )A. | B. |
C. | D. |
C
试题分析:因为
 ,所以
,所以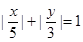 ,此方程表示的图像是由椭圆
,此方程表示的图像是由椭圆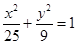 的四个顶点组成的四边形,显然在椭圆内部(除顶点外),因而
的四个顶点组成的四边形,显然在椭圆内部(除顶点外),因而 .
.点评:解本小题的突破口是把方程
 ,化成
,化成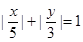 作出其图像,可知它是由椭圆
作出其图像,可知它是由椭圆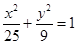 的四个顶点组成的四边形, 显然在椭圆内部(除顶点外),再结合双曲线的定义可知
的四个顶点组成的四边形, 显然在椭圆内部(除顶点外),再结合双曲线的定义可知 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
 是曲线
是曲线 上的点,
上的点, ,则( )
,则( )A. | B. |
C. | D. |
 ,所以
,所以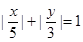 ,此方程表示的图像是由椭圆
,此方程表示的图像是由椭圆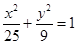 的四个顶点组成的四边形,显然在椭圆内部(除顶点外),因而
的四个顶点组成的四边形,显然在椭圆内部(除顶点外),因而 .
. ,化成
,化成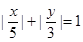 作出其图像,可知它是由椭圆
作出其图像,可知它是由椭圆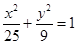 的四个顶点组成的四边形, 显然在椭圆内部(除顶点外),再结合双曲线的定义可知
的四个顶点组成的四边形, 显然在椭圆内部(除顶点外),再结合双曲线的定义可知 .
.
 名校课堂系列答案
名校课堂系列答案