题目内容
设函数
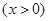 ,其中
,其中 ,
, 为正整数,
为正整数,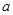 ,
, ,
, 均为常数,曲线
均为常数,曲线 在
在 处的切线方程为
处的切线方程为 .
.
(1)求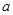 ,
, ,
, 的值;
的值;
(2)求函数 的最大值;
的最大值;
(3)证明:对任意的 都有
都有 .(
.( 为自然对数的底)
为自然对数的底)

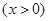 ,其中
,其中 ,
, 为正整数,
为正整数,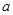 ,
, ,
, 均为常数,曲线
均为常数,曲线 在
在 处的切线方程为
处的切线方程为 .
.(1)求
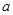 ,
, ,
, 的值;
的值; (2)求函数
 的最大值;
的最大值;(3)证明:对任意的
 都有
都有 .(
.( 为自然对数的底)
为自然对数的底)(1) ;(2)
;(2)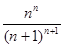 ;(3)见解析.
;(3)见解析.
 ;(2)
;(2)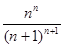 ;(3)见解析.
;(3)见解析.试题分析:(1)在切点处的的函数值
 ,就是切线
,就是切线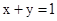 的斜率为
的斜率为 ,可得
,可得 ;根据切点适合切线方程、曲线方程,可得
;根据切点适合切线方程、曲线方程,可得 ,
, .
.(2)求导数,求驻点,讨论区间函数单调性,确定最值.
(3)本小题有多种思路,一是要证对任意的
 都有
都有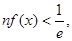 只需证
只需证
 ;
;二是令
 ,利用导数确定
,利用导数确定 ,
,转化得到
 .
.令
 ,证明
,证明 .
.(1)因为
 , 1分
, 1分所以
 ,又因为切线
,又因为切线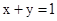 的斜率为
的斜率为 ,所以
,所以 2分
2分 ,由点(1,c)在直线
,由点(1,c)在直线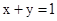 上,可得
上,可得 ,即
,即 3分
3分 4分
4分(2)由(1)知,
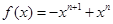 ,所以
,所以
令
 ,解得
,解得
 ,即
,即 在(0,+
在(0,+ 上有唯一零点
上有唯一零点
 5分
5分当0<
 <
< 时,
时, ,故
,故 在(0,
在(0, )上单调递增; 6分
)上单调递增; 6分当
 >
> 时,
时, ,故
,故 在(
在( ,+
,+ 上单调递减; 7分
上单调递减; 7分 在(0,+
在(0,+ 上的最大值
上的最大值 =
= =
=
 =
=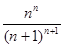 8分
8分(3)证法1:要证对任意的
 都有
都有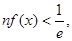 只需证
只需证

由(2)知在
 上
上 有最大值,
有最大值, =
= ,故只需证
,故只需证
 9分
9分
 ,即
,即
 ① 11分
① 11分令

 ,则
,则 ,①即
,①即 ② 13分
② 13分令
 ,则
,则
显然当0<t<1时,
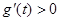 ,所以
,所以 在(0,1)上单调递增,
在(0,1)上单调递增,所以
 ,即对任意的
,即对任意的 ②恒成立,
②恒成立,所以对任意的
 都有
都有 14分
14分证法2:令
 ,则
,则 . 10分
. 10分当
 时,
时, ,故
,故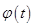 在
在 上单调递减;
上单调递减;而当
 时,
时, ,故
,故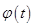 在
在 上单调递增.
上单调递增. 在
在 上有最小值,
上有最小值, .
. ,即
,即 . 12分
. 12分令
 ,得
,得 ,即
,即 ,所以
,所以 ,即
,即 .
.由(2)知,
 ,故所证不等式成立. 14分
,故所证不等式成立. 14分
练习册系列答案
相关题目


 (单位:天)变化的函数关系式近似为
(单位:天)变化的函数关系式近似为 若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用. )个单位的药剂,要使接下来的4天中能够持续有效净化,试求
)个单位的药剂,要使接下来的4天中能够持续有效净化,试求 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据: 取1.4).
取1.4).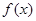 定义在
定义在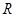 上,对任意的
上,对任意的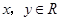 ,
,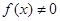 ,且
,且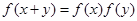 .
.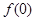 ,并证明:
,并证明: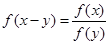 ;
;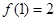 .设向量
.设向量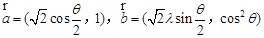 ,对任意
,对任意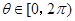 ,
,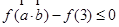 恒成立,求实数
恒成立,求实数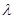 的取值范围.
的取值范围. +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称. 在
在 内 ( )
内 ( ) km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
 ,若f(-4)=f(0),f(-2)=0,则关于x的不等式f(x)≤1的解集为( )
,若f(-4)=f(0),f(-2)=0,则关于x的不等式f(x)≤1的解集为( )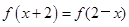 ,则
,则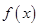 的图象关于
的图象关于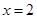 对称;
对称;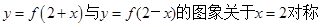 ;
;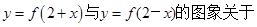 y轴对称。正确命题的序号是 .
y轴对称。正确命题的序号是 .