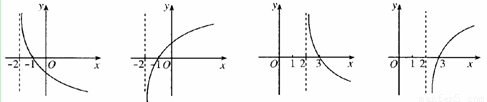
题目内容
若函数f(x)=(k-1)(
)x-2x在R上是奇函数,则(g)x=log
(x+k)的图象是( )
| 1 |
| 2 |
| 1 |
| 2 |
分析:先结合对数函数是奇函数性质将k确定,然后代入函数g(x)在进行图象变换即可获得解答.
解答:解:∵f(x)=(k-1)(
)x-2x在R上是奇函数
由奇函数的性质可知,f(0)=k-1-1=0
∴k=2
∴g(x)=log
(x+2)
∵g(x)的图象可由函数y=log
x的图象向左平移2个单位可得
故选A
| 1 |
| 2 |
由奇函数的性质可知,f(0)=k-1-1=0
∴k=2
∴g(x)=log
| 1 |
| 2 |
∵g(x)的图象可由函数y=log
| 1 |
| 2 |
故选A
点评:此题考查的是对数函数的图象和性质问题以及图象变换的问题.在解答的过程当中既考查到了函数的奇偶性也体现了图象变换在问题中应用.

练习册系列答案
相关题目
若函数f(x)=
在定义域上为奇函数,则实数k的值为( )
| k-2x |
| 1+k?2x |
| A、±1 | B、-1 | C、1 | D、0或±1 |