题目内容
(14分)已知向量![]() ,其中
,其中![]() ,
,![]() ,把其中x,y所
,把其中x,y所
满足的关系式记为y=f(x),若f(x)为奇函数。
(1)求函数f(x)的表达式;
(2)已知数列{an}的各项都是正数,Sn为数列{an}的前n项和,且对于任意n∈N*,都
有{f(an)}的前n项和等于Sn2,求数列{an}的通项公式。
(3)若数列{bn}满足bn=4n-a?2 an+1(a∈R),求数列{bn}的最小值.
解析:(1)∵![]() ∥
∥![]() ∴
∴![]() ,因为函数f(x)
,因为函数f(x)
为奇![]() 函数。所以c=1,
函数。所以c=1,![]() ???4分
???4分
(2)由题意可知,f(a1)+ f(a2)+???+ f(an)=![]() ①
①
![]() 时 ∴
时 ∴![]() ②
②
由①―②可得:
![]()
∵{an}为正数数列∴![]() ③
③
∴![]() ④
④
由④―③可得:![]()
∵![]()
且由①可得![]()
∴a1-a2=1 ∴{an}为公差为1的等差数列,
∴an=n(n∈N*) ???8分
(3)∵an=n(n∈N*),∴bn=4n-a?2 n+1=(2 n-a) 2-a2(n∈N*)
令2 n=t(t![]() 2),∴bn=
2),∴bn=![]()
(1)当![]() 时,数列{bn}的最小值为:当n=1时,b1=4-4a
时,数列{bn}的最小值为:当n=1时,b1=4-4a
(2)当a>2时
①若![]() N*)时,数列{bn}的最小值为当n=k+1时,bk+1=-a2。
N*)时,数列{bn}的最小值为当n=k+1时,bk+1=-a2。
②若![]() (k∈N*),数列{bn}的最小值为
(k∈N*),数列{bn}的最小值为
当n=k或n=k+1时,![]()
③若![]() (k∈N*),数列{bn}的最小值为
(k∈N*),数列{bn}的最小值为
当n=k时,bk=(2k-a)2-a2
④若![]() (k∈N*),数列{bn}的最小值为
(k∈N*),数列{bn}的最小值为

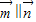 ,其中
,其中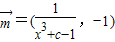 ,
,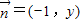 (x,y,c∈R),把其中x,y所满足的关系式记为y=f(x),若函数f(x)为奇函数.
(x,y,c∈R),把其中x,y所满足的关系式记为y=f(x),若函数f(x)为奇函数.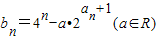 ,求数列{bn}的最小值.
,求数列{bn}的最小值.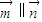 ,其中
,其中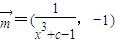 ,
,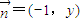 (x,y,c∈R),把其中x,y所满足的关系式记为y=f(x),若函数f(x)为奇函数.
(x,y,c∈R),把其中x,y所满足的关系式记为y=f(x),若函数f(x)为奇函数.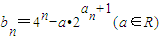 ,求数列{bn}的最小值.
,求数列{bn}的最小值.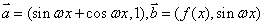 ,其中
,其中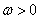 ,已知函数
,已知函数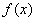 的周期
的周期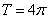 ,且
,且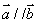
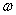 的值;
的值;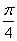 个单位,得到函数
个单位,得到函数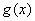 的图象,求
的图象,求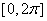 上的单调递增区间。
上的单调递增区间。