题目内容
已知向量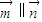 ,其中
,其中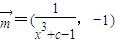 ,
,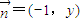 (x,y,c∈R),把其中x,y所满足的关系式记为y=f(x),若函数f(x)为奇函数.
(x,y,c∈R),把其中x,y所满足的关系式记为y=f(x),若函数f(x)为奇函数.(Ⅰ) 求函数f(x)的表达式;
(Ⅱ) 已知数列{an}的各项都是正数,Sn为数列{an}的前n项和,且对于任意n∈N*,都有“{f(an)}的前n项和等于Sn2,”求数列{an}的通项式;
(Ⅲ) 若数列{bn}满足
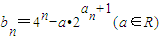 ,求数列{bn}的最小值.
,求数列{bn}的最小值.
【答案】分析:(Ⅰ)根据向量平行得出函数y=f(x),再利用函数f(x)为奇函数,可求c=1,从而可得函数f(x)的表达式;
(Ⅱ) 根据条件对于任意n∈N*,都有“{f(an)}的前n项和等于Sn2,写出两等式,两式相减可得∴{an}为公差为1的等差数列,从而可求数列{an}的通项公式;
(Ⅲ)根据an=n(n∈N*),可得bn=4n-a•2n+1=(2n-a)2-a2,由于2n≥2,故需对a进行分类讨论.
解答:解:(Ⅰ)∵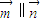 ∴
∴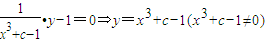 ,
,
因为函数f(x)为奇函数.所以c=1,⇒f(x)=x3(x≠0)…(4分)
(Ⅱ)由题意可知,f(a1)+f(a2)+…+f(an)=Sn2⇒a13+a23+a33+…+an3=Sn2…..①
n≥2时∴a13+a23+a33+…+an-13=Sn-12…②
由①-②可得:an3=Sn2-Sn-12=an(Sn+Sn-1),
∵{an}为正数数列∴an2=Sn+Sn-1…③…(2分)∴an+12=Sn+1+Sn…④
由④-③可得:an+12-an2=an+1+an∵an+1+an>0,∴an+1-an=1,…(2分)
且由①可得a13=a12,a1>0⇒a1=1,a13+a23=S22,a2>0⇒a2=2,∴a2-a1=1∴{an}为公差为1的等差数列,∴an=n(n∈N*)…(2分)
(Ⅲ)∵an=n(n∈N*),∴bn=4n-a•2n+1=(2n-a)2-a2(n∈N*)…(2分)
令2n=t(t≥2),∴bn=(t-a)2-a2(t≥2)
(1)当a≤2时,数列{bn}的最小值为:当n=1时,b1=4-4a.…(2分)
(2)当a>2时
①若a=2k+1(k∈N*)时,数列{bn}的最小值为当n=k+1时,bk+1=-a2.…(1分)
②若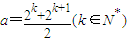 时,数列{bn}的最小值为,当n=k或n=k+1时,bk=bk+1=(2k-a)2-a2.…(1分)
时,数列{bn}的最小值为,当n=k或n=k+1时,bk=bk+1=(2k-a)2-a2.…(1分)
③若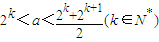 时,数列{bn}的最小值为,当n=k时,bk=(2k-a)2-a2…(1分)
时,数列{bn}的最小值为,当n=k时,bk=(2k-a)2-a2…(1分)
④若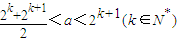 时,数列{bn}的最小值为,当n=k+1时,bk+1=(2k+1-a)2-a2.…(1分)
时,数列{bn}的最小值为,当n=k+1时,bk+1=(2k+1-a)2-a2.…(1分)
点评:本题的考点是数列与向量的综合,主要考查向量共线条件的运用,考查数列通项公式的求解,考查了函数的最值,关键是正确分类.
(Ⅱ) 根据条件对于任意n∈N*,都有“{f(an)}的前n项和等于Sn2,写出两等式,两式相减可得∴{an}为公差为1的等差数列,从而可求数列{an}的通项公式;
(Ⅲ)根据an=n(n∈N*),可得bn=4n-a•2n+1=(2n-a)2-a2,由于2n≥2,故需对a进行分类讨论.
解答:解:(Ⅰ)∵
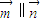 ∴
∴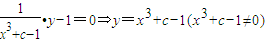 ,
,因为函数f(x)为奇函数.所以c=1,⇒f(x)=x3(x≠0)…(4分)
(Ⅱ)由题意可知,f(a1)+f(a2)+…+f(an)=Sn2⇒a13+a23+a33+…+an3=Sn2…..①
n≥2时∴a13+a23+a33+…+an-13=Sn-12…②
由①-②可得:an3=Sn2-Sn-12=an(Sn+Sn-1),
∵{an}为正数数列∴an2=Sn+Sn-1…③…(2分)∴an+12=Sn+1+Sn…④
由④-③可得:an+12-an2=an+1+an∵an+1+an>0,∴an+1-an=1,…(2分)
且由①可得a13=a12,a1>0⇒a1=1,a13+a23=S22,a2>0⇒a2=2,∴a2-a1=1∴{an}为公差为1的等差数列,∴an=n(n∈N*)…(2分)
(Ⅲ)∵an=n(n∈N*),∴bn=4n-a•2n+1=(2n-a)2-a2(n∈N*)…(2分)
令2n=t(t≥2),∴bn=(t-a)2-a2(t≥2)
(1)当a≤2时,数列{bn}的最小值为:当n=1时,b1=4-4a.…(2分)
(2)当a>2时
①若a=2k+1(k∈N*)时,数列{bn}的最小值为当n=k+1时,bk+1=-a2.…(1分)
②若
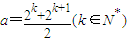 时,数列{bn}的最小值为,当n=k或n=k+1时,bk=bk+1=(2k-a)2-a2.…(1分)
时,数列{bn}的最小值为,当n=k或n=k+1时,bk=bk+1=(2k-a)2-a2.…(1分)③若
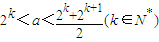 时,数列{bn}的最小值为,当n=k时,bk=(2k-a)2-a2…(1分)
时,数列{bn}的最小值为,当n=k时,bk=(2k-a)2-a2…(1分)④若
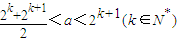 时,数列{bn}的最小值为,当n=k+1时,bk+1=(2k+1-a)2-a2.…(1分)
时,数列{bn}的最小值为,当n=k+1时,bk+1=(2k+1-a)2-a2.…(1分)点评:本题的考点是数列与向量的综合,主要考查向量共线条件的运用,考查数列通项公式的求解,考查了函数的最值,关键是正确分类.

练习册系列答案
相关题目
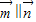 ,其中
,其中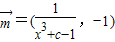 ,
,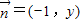 (x,y,c∈R),把其中x,y所满足的关系式记为y=f(x),若函数f(x)为奇函数.
(x,y,c∈R),把其中x,y所满足的关系式记为y=f(x),若函数f(x)为奇函数.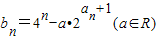 ,求数列{bn}的最小值.
,求数列{bn}的最小值.