题目内容
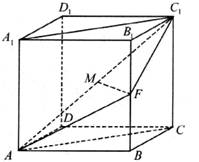
已知直四棱柱ABCD—A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,M为线段AC1的中点。
(1)求证:直线MF∥平面ABCD;
(2)求证:平面AFC1⊥平面ACC1A1;
(3)求平面AFC1与平面ABCD所成二面角的大小。
【答案】
(1)延长C1F交CB的延长线于点N,连接AN。
因为F是BB1的中点,所以F为C1N的中点,B为CN的中点
又因为M是线段AC1的中点,故MF∥AN
∴MF∥平面ABCD
(2)连接BD,由直四棱柱ABCD—A1B1C1D1,可知:
∵四边形ABCD为菱形,∴AC⊥BD
又∵AC∩A1A=A,AC,A1A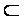 平面ACC1A1,∴BD⊥平面ACC1A1
平面ACC1A1,∴BD⊥平面ACC1A1
在四边形DANB中,DA∥BN且DA=BN,所以四边形DANB为平行四边形
故NA∥BD,∴NA⊥平面ACC1A1
(3)由(2)知BD⊥ACC1A1,又AC1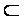 ACC1A1,∴BD⊥AC1
ACC1A1,∴BD⊥AC1
∵BD∥NA,∴AC1⊥NA
又由BD⊥AC可知NA⊥AC
∴∠C1AC就是平面AFC1与平面ABCD所成二面角的平面角或补角
平面AFC1与平面ABCD所成二面角的大小为30°或150°。
(说明:求对一个角即给满分)

练习册系列答案
相关题目


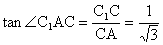
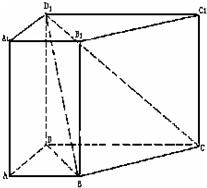 已知直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB=AD=1,DD1=CD=2,AB⊥AD.
已知直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB=AD=1,DD1=CD=2,AB⊥AD.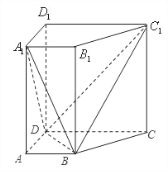 如图所示,已知直四棱柱ABCD-A1B1C1D1中,AD⊥DCAB∥DC,且满足
如图所示,已知直四棱柱ABCD-A1B1C1D1中,AD⊥DCAB∥DC,且满足 如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求:
如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求: 已知直四棱柱ABCD-A1B1C1D1的底面是菱形,F为棱BB1的中点,M为线段AC1的中点.
已知直四棱柱ABCD-A1B1C1D1的底面是菱形,F为棱BB1的中点,M为线段AC1的中点. (2010•宝山区模拟)已知直四棱柱ABCD-A1B1C1D1体积为32,且底面四边形ABCD为直角梯形,其中上底BC=2,下底AD=6,腰AB=2,且BC⊥AB.
(2010•宝山区模拟)已知直四棱柱ABCD-A1B1C1D1体积为32,且底面四边形ABCD为直角梯形,其中上底BC=2,下底AD=6,腰AB=2,且BC⊥AB.