题目内容
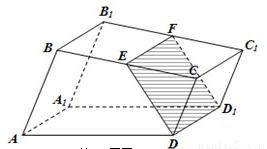
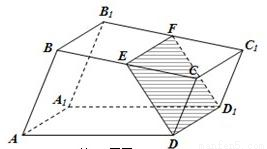
 如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求:
如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求:(1)截面PBD分这个棱柱所得的两个几何体的体积;
(2)三棱锥A-PBD的高.
分析:(1)利用棱锥的体积,求出底面面积,然后求出棱锥的体积,求出棱柱的体积.
(2)利用等体积法,求出棱锥的高即可.
(2)利用等体积法,求出棱锥的高即可.
解答:解:(1)因为直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,
AA1=6,P是棱AA1的中点.所以S底=
×4×4sin60°=4
,V锥=
×3×4
=4
.
V多面体=V柱-V锥=2×4
×6-4
=44
.
(2)S△PBD=
BD•
=
×4×
=2
,
因为VP-ABD=VA-PBD,
所以4
=
×2
h,
h=
.
三棱锥A-PBD的高为
.
AA1=6,P是棱AA1的中点.所以S底=
| 1 |
| 2 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
V多面体=V柱-V锥=2×4
| 3 |
| 3 |
| 3 |
(2)S△PBD=
| 1 |
| 2 |
PA2+AB2-(
|
| 1 |
| 2 |
| 9+12 |
| 21 |
因为VP-ABD=VA-PBD,
所以4
| 3 |
| 1 |
| 3 |
| 21 |
h=
6
| ||
| 7 |
三棱锥A-PBD的高为
6
| ||
| 7 |
点评:本题考查棱柱、棱锥、棱台的体积,棱柱的结构特征,考查计算能力.

练习册系列答案
相关题目
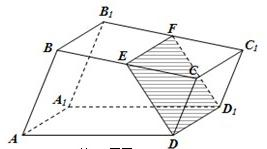 如图,已知直四棱柱ABCD-A1B1C1D1的底面是直角梯形,AB⊥BC,AB∥CD,E,F分别是棱BC,B1C1上的动点,且EF∥CC1,CD=DD1=1,AB=2,BC=3.
如图,已知直四棱柱ABCD-A1B1C1D1的底面是直角梯形,AB⊥BC,AB∥CD,E,F分别是棱BC,B1C1上的动点,且EF∥CC1,CD=DD1=1,AB=2,BC=3.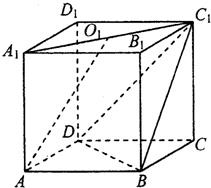 如图,已知直四棱柱ABCD-A1B1C1D1的底面边长和侧棱长均为1,且满足∠BAD=60°,O1为A1C1的中点.
如图,已知直四棱柱ABCD-A1B1C1D1的底面边长和侧棱长均为1,且满足∠BAD=60°,O1为A1C1的中点.