题目内容
（2012•湖北模拟）已知l是直线，α、β是两个不同的平面，命题p：l∥α，l⊥β，则α⊥β；命题q：α⊥β，l⊥β则l∥α；命题r：α⊥β，l∥α，则l⊥β，则下列命题中，真命题是（ ）
分析：先判断命题p、q、r的真假，然后再利用“或”、“且”、“非”的真假法则判断即可．
解答：解：①命题p：l∥α，l⊥β，则α⊥β．正确．下面给出证明：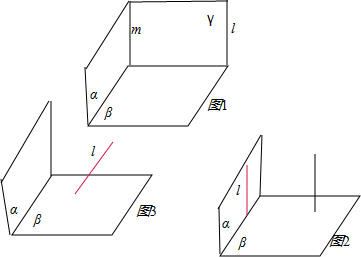
如图所示：过直线l作平面γ∩α=m，∵l∥α，∴l∥m．
∵l⊥β，∴m⊥β，
由m?α，∴α⊥β．故命题p正确．
②命题q：α⊥β，l⊥β则l∥α；如图2，可能l?α，故命题q是假命题．
③命题r：α⊥β，l∥α，则l⊥β．如图3，直线l可能与平面β平行、在平面β内或相交，故命题r是假命题．
综上可知：p真，q假，r假．
故p∧q假，qVr假，pVq真，￢p假．
故真命题是C．
故选C．
如图所示：过直线l作平面γ∩α=m，∵l∥α，∴l∥m．
∵l⊥β，∴m⊥β，
由m?α，∴α⊥β．故命题p正确．
②命题q：α⊥β，l⊥β则l∥α；如图2，可能l?α，故命题q是假命题．
③命题r：α⊥β，l∥α，则l⊥β．如图3，直线l可能与平面β平行、在平面β内或相交，故命题r是假命题．
综上可知：p真，q假，r假．
故p∧q假，qVr假，pVq真，￢p假．
故真命题是C．
故选C．
点评：正确判断命题p、q、r的真假和理解“或”、“且”、“非”的真假判断法则是解题的关键．
练习册系列答案
相关题目
（2012•湖北模拟）已知函数y=g（x）的图象由f（x）=sin2x的图象向右平移φ（0＜φ＜π）个单位得到，这两个函数的部分图象如图所示，则φ=