题目内容
在平面几何中,三角形、梯形的面积可以通过下述公式:
S三角形=
×a底×h高,S梯形=
×h高 来求得.
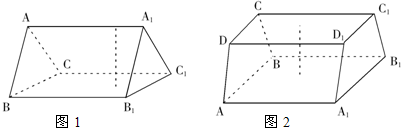
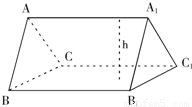
类比到立体几何中,将一个侧面放置在水平面上的一个三棱柱与一个四棱柱(底面是梯形)
如图,图(1)、图(2)中的体积计算公式分别是:
×S底×h高
×S底×h高;
×h高
×h高.
S三角形=
| 1 |
| 2 |
| a上底+b下底 |
| 2 |

类比到立体几何中,将一个侧面放置在水平面上的一个三棱柱与一个四棱柱(底面是梯形)
如图,图(1)、图(2)中的体积计算公式分别是:
| 1 |
| 2 |
| 1 |
| 2 |
| S 上底+S 下底 |
| 2 |
| S 上底+S 下底 |
| 2 |
分析:根据平面与空间之间的类比推理,由点类比点或直线,由直线 类比 直线或平面,由三角形类比三棱柱,由梯形类比四棱柱,由平面图形面积类比立体图形的体积,结合求三角形、梯形的面积的方法类比求三棱柱与一个四棱柱的体积即可.
解答: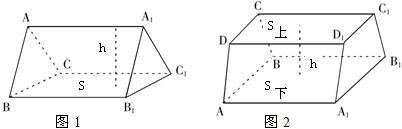 解:由三角形类比三棱柱,由梯形类比四棱柱,由平面图形面积类比立体图形的体积,结合求三角形、梯形的面积的方法类比求三棱柱与一个四棱柱的体积:
解:由三角形类比三棱柱,由梯形类比四棱柱,由平面图形面积类比立体图形的体积,结合求三角形、梯形的面积的方法类比求三棱柱与一个四棱柱的体积:
如图,设三棱柱侧棱AA1到面BB1C1C的距离为h高,四边形BB1C1C的面积为S.
则其体积V三棱柱=
×S底×h高,
与一个四棱柱V四棱柱=
×h高
故答案为:
×S底×h高;
×h高
 解:由三角形类比三棱柱,由梯形类比四棱柱,由平面图形面积类比立体图形的体积,结合求三角形、梯形的面积的方法类比求三棱柱与一个四棱柱的体积:
解:由三角形类比三棱柱,由梯形类比四棱柱,由平面图形面积类比立体图形的体积,结合求三角形、梯形的面积的方法类比求三棱柱与一个四棱柱的体积:如图,设三棱柱侧棱AA1到面BB1C1C的距离为h高,四边形BB1C1C的面积为S.
则其体积V三棱柱=
| 1 |
| 2 |
与一个四棱柱V四棱柱=
| S 上底+S 下底 |
| 2 |
故答案为:
| 1 |
| 2 |
| S 上底+S 下底 |
| 2 |
点评:本题主要考查类比推理.类比推理是指依据两类数学对象的相似性,将已知的一类数学对象的性质类比迁移到另一类数学对象上去.一般步骤:①找出两类事物之间的相似性或者一致性.②用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(或猜想).

练习册系列答案
相关题目
 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2, C.
C. 在平面几何中,三角形的面积可以通过公式:S三角形=
在平面几何中,三角形的面积可以通过公式:S三角形= ×a底×h高,S梯形=
×a底×h高,S梯形=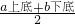 ×h高 来求得.
×h高 来求得.
 a底h高来求得:类比到立体几何中,将一个侧面放置在水平面上的三棱柱(如图),其体积计算公式是 .
a底h高来求得:类比到立体几何中,将一个侧面放置在水平面上的三棱柱(如图),其体积计算公式是 .