题目内容
【题目】若函数![]() 的导函数
的导函数![]() ,
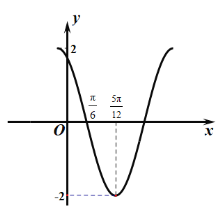
,![]() 的部分图象如图所示,
的部分图象如图所示,![]() ,当
,当![]() ,
,![]() 时,则
时,则![]() 的最大值为_________.
的最大值为_________.
【答案】![]()
【解析】
由图象可得:A=2,![]() ,解得ω=2.可得f′(x)=2cos(2
,解得ω=2.可得f′(x)=2cos(2![]() φ)=﹣2,|φ|
φ)=﹣2,|φ|![]() ),把x
),把x![]() ,
,![]() 2代入解得φ.可得f′(x),进而得出f(x),g(x)=f(x
2代入解得φ.可得f′(x),进而得出f(x),g(x)=f(x![]() ),利用正弦函数的单调性即可得出结论.
),利用正弦函数的单调性即可得出结论.
由图象可得:A=2,![]() ,解得ω=2.
,解得ω=2.
∴f′(x)=2cos(2![]() φ)=﹣2,|φ|
φ)=﹣2,|φ|![]() ),解得φ
),解得φ![]() .
.
∴f′(x)=2cos(2x![]() ).
).
∴f(x)=sin(2x![]() )+c.(c为常数).
)+c.(c为常数).
g(x)=f(x![]() )=sin2x+c.
)=sin2x+c.
x∈[![]() ,
,![]() ]时,2x∈
]时,2x∈![]() .
.
sin2x∈![]() ,
,
当x1,x2∈[![]() ,
,![]() ]时,则|g(x1)﹣g(x2)|=|sin2x1﹣sin2x2|≤1﹣(
]时,则|g(x1)﹣g(x2)|=|sin2x1﹣sin2x2|≤1﹣(![]() )
)![]() .
.
因此当x1,x2∈[![]() ,
,![]() ]时,则|g(x1)﹣g(x2)|的最大值为
]时,则|g(x1)﹣g(x2)|的最大值为![]() .
.
故答案为![]() .
.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目