题目内容
某篮球联赛的总决赛在甲、乙两队之间角逐.采用七场四胜制,即有一队胜四场,则此队获胜,同时比赛结束.在每场比赛中,两队获胜的概率相等.根据以往资料统计,每场比赛组织者可获门票收入32万元,两队决出胜负后,问:(Ⅰ)组织者在此次决赛中,获门票收入为128万元的概率是多少?
(Ⅱ)设组织者在此次决赛中获门票收入为ξ,求ξ的分布列及Eξ.
解:(I)甲、乙两队获胜的概率相同甲、乙两队获胜的概率都是![]() 又此决赛中获门票收入为128万元
又此决赛中获门票收入为128万元
∴比赛恰好进行四场(2分)甲胜四场的概率为![]() ,乙胜四场的概率为
,乙胜四场的概率为![]()
![]() +
+![]() =
=![]()
答:组织者在此决赛中获门票收入为128万元的概率是![]()
(Ⅱ)因为比赛可能进行四场、五场、六场或七场所以ζ的取值为128,160,192,224
P(ζ=128)=![]()
P(ζ=160)=2![]()
P(ζ=192)=2![]()
p(ζ=224)=2![]()
ζ | 128 | 160 | 192 | 224 |
P |
|
|
|
|
Eζ=128×![]() +160×
+160×![]() +192×
+192×![]() +224×
+224×![]() =186.
=186.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
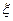 ,求
,求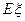 。
。