题目内容
a<0是方程 至少有一个负数根的( )
至少有一个负数根的( )
| A.必要不充分条件 | B.充分不必要条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
B
解析试题分析:由于方程 至少有一个负数根,包括有三种情况,只有一个负根,当a=0时,显然成立;一个负根和一个正根,以及两个负数根,当一正一负时,满足
至少有一个负数根,包括有三种情况,只有一个负根,当a=0时,显然成立;一个负根和一个正根,以及两个负数根,当一正一负时,满足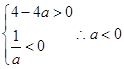 ,当有两个负数根时,则满足
,当有两个负数根时,则满足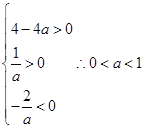 ,综上可知满足题意的a<1,因此条件是结论成立的充分不必要条件
,综上可知满足题意的a<1,因此条件是结论成立的充分不必要条件
选B.
考点:本试题考查了充分条件的判定的运用。
点评:解决该试题的关键是对于一元二次方程中根与系数的关系的理解和准确的表示运用,注意同时要分类讨论得到各个情况下的满足题意的a的范围,结合充分条件来判定得到,属于基础题。

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
已知命题p: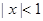 ,命题q:
,命题q: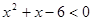 ,则
,则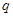 是
是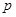 成立的 ( )
成立的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列有关命题的说法正确的是 ( )
A.命题“若 ,则 ,则 ”的否命题为:“若 ”的否命题为:“若 ,则 ,则 ”. ”. |
B.“ ”是“ ”是“ ”的必要不充分条件. ”的必要不充分条件. |
C.命题“ 使得 使得 ”的否定是:“ ”的否定是:“ 均有 均有 ”. ”. |
D.命题“若 ,则 ,则 ”的逆否命题为真命题. ”的逆否命题为真命题. |
设 ,则“
,则“ 且
且 ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
“a和b都不是奇数”的否定是( )
| A.a和b至少有一个奇数 | B.a和b至多有一个是奇数 |
| C.a是奇数,b不是奇数 | D.a和b都是奇数 |
某学习小组对函数 进行研究,得出了如下四个结论:①函数
进行研究,得出了如下四个结论:①函数 在
在 上单调递增;②存在常数
上单调递增;②存在常数 对一切实数
对一切实数 均成立;③函数
均成立;③函数 在
在 上无最小值,但一定有最大值;④点
上无最小值,但一定有最大值;④点 是函数
是函数 的一个对称中心,其中正确的是
的一个对称中心,其中正确的是
| A.①③ | B.②③ | C.②④ | D.①②④ |
下列命题中,是真命题的是( )
A. | B. |
C. | D. |
“ ”是“直线
”是“直线 与直线
与直线 平行”的( )
平行”的( )
| A.充分必要条件 | B.充分而不必要条件 |
| C.必要而不充分条件 | D.既不充分也不必要条件 |
若命题p: ,则┑p 为( )
,则┑p 为( )
A. | B. |
C. | D. |