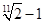题目内容
设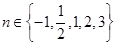 ,则使得
,则使得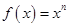 为奇函数,且在
为奇函数,且在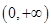 上单调递减的
上单调递减的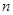 的个数为
的个数为
| A.1 | B.2 | C.3 | D.4 |
A
解析试题分析:根据幂函数的指数大于0,则在区间(0,+∞)上单调递增,可排除n= ,1,2,3的可能,然后判定当n=-1时,f(x)=
,1,2,3的可能,然后判定当n=-1时,f(x)= 是否满足条件即可.解:f(x)=xn,当n>0时函数f(x)在区间(0,+∞)上单调递增,故
是否满足条件即可.解:f(x)=xn,当n>0时函数f(x)在区间(0,+∞)上单调递增,故 ,1,2,3都不符合题意,当n=-1时,f(x)=
,1,2,3都不符合题意,当n=-1时,f(x)= ,定义域为{x|x≠0},f(-x)=-
,定义域为{x|x≠0},f(-x)=- =-f(x),在区间(0,+∞)上单调递减,故正确,故选A
=-f(x),在区间(0,+∞)上单调递减,故正确,故选A
考点:幂函数的性质
点评:本题主要考查了幂函数的性质,同时考查了函数奇偶性的判定,属于基础题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
已知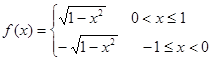 且
且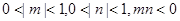 ,则使不等式
,则使不等式
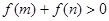 成立的m和n还应满足条件是( )
成立的m和n还应满足条件是( )
A.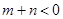 | B.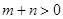 | C. | D.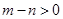 |
已知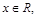 符号
符号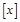 表示不超过
表示不超过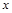 的最大整数,若函数
的最大整数,若函数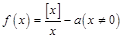 有且仅有3个零点,则
有且仅有3个零点,则 的取值范围是( )
的取值范围是( )
A. | B. |
C.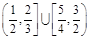 | D.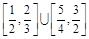 |
已知函数 ,给出下列四个命题:
,给出下列四个命题:
①若 ②
② 的最小正周期是
的最小正周期是 ;
;
③ 在区间
在区间 上是增函数; ④
上是增函数; ④ 的图象关于直线
的图象关于直线 对称;
对称;
⑤当 时,
时, 的值域为
的值域为 其中正确的命题为
其中正确的命题为
| A.①②④ | B.③④⑤ | C.②③ | D.③④ |
下列函数既是奇函数,又在区间 上单调递减的是( )
上单调递减的是( )
A.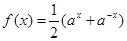 | B.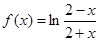 |
C.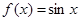 | D. |
设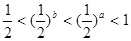 ,那么
,那么
A. | B. | C. | D.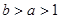 |
设函数f(x)= ,若f(x0)>1,则x0的取值范围为( )
,若f(x0)>1,则x0的取值范围为( )
A.(-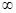 ,-1)∪(1,+ ,-1)∪(1,+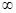 ) ) | B.(-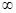 ,-1)∪[1,+ ,-1)∪[1,+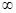 ) ) |
C.(-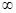 ,-3)∪(1,+ ,-3)∪(1,+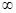 ) ) | D.(-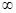 ,-3)∪[1,+ ,-3)∪[1,+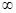 ) ) |
函数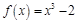 的零点所在的区间是( )
的零点所在的区间是( )
A.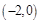 | B.(0,1) | C.(1,2) | D.(2,3) |