题目内容
已知函数
(1)当 时,求函数
时,求函数 的最小值和最大值
的最小值和最大值
(2)设三角形角 的对边分别为
的对边分别为 且
且 ,
,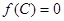 ,若
,若 ,求
,求 的值.
的值.
(1)最小值为 ,最大值为0;(2)
,最大值为0;(2) .
.
解析试题分析:(1)先通过三角函数的恒等变形化 的形式后再解答;一般地,涉及三角函数的值域问题,多数情况下要将其变形为
的形式后再解答;一般地,涉及三角函数的值域问题,多数情况下要将其变形为 后,再利用三角函数的性质解答,也有部分题目,可转化为角的某个三角函数,然后用换元法转化为非三角函数问题;(2)由
后,再利用三角函数的性质解答,也有部分题目,可转化为角的某个三角函数,然后用换元法转化为非三角函数问题;(2)由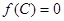 先求出
先求出 ,再利用正弦定理求出
,再利用正弦定理求出 ,再利用余弦定理则可求出
,再利用余弦定理则可求出 .在三角形中求角或边,通常对条件进行“统一”,统一为边或统一为角,主要的工具是正弦定理和余弦定理,同时不要忘记了三角形内角和定理.
.在三角形中求角或边,通常对条件进行“统一”,统一为边或统一为角,主要的工具是正弦定理和余弦定理,同时不要忘记了三角形内角和定理.
试题解析:(1)
 ,因为
,因为  ,
, ,所以当
,所以当 时,
时, 取得最小值
取得最小值 ,当
,当 时,
时, 取得最大值0 6分
取得最大值0 6分
(2)由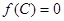 ,得
,得 ,又
,又 为三角形内角,所以
为三角形内角,所以 ,所以
,所以 ,由正弦定理结合
,由正弦定理结合 得,
得, ,再由余弦定理
,再由余弦定理 得,
得,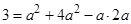 ,解得
,解得 ,所以
,所以 13分
13分
考点:三角函数性质、正弦定理、余弦定理.

练习册系列答案
相关题目

 中,角A、B,C,所对的边分别为
中,角A、B,C,所对的边分别为 ,且
,且
 的值;
的值; ,求
,求 的最大值为2.
的最大值为2. 在
在 上的单调递减区间;
上的单调递减区间; 中,
中, ,角
,角 所对的边分别是
所对的边分别是 ,且
,且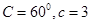 ,求
,求 ,BC=1,P为△ABC内一点,∠BPC=90°
,BC=1,P为△ABC内一点,∠BPC=90°
 ,求PA;
,求PA; .
. ,求该三角形内切圆半径的取值范围。
,求该三角形内切圆半径的取值范围。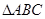 三个内角
三个内角 的对边分别为
的对边分别为 ,向量
,向量 ,
, ,且
,且 与
与 的夹角为
的夹角为 .
. 的值;
的值; ,
, ,求
,求 的值.
的值. 中,其中
中,其中 为定点,
为定点, 为动点,满足
为动点,满足 .
. 与
与 的关系式;
的关系式; 的面积分别为
的面积分别为 和
和 ,求
,求 的最大值,以及此时凸四边形
的最大值,以及此时凸四边形 ,
, ,
, ,
, ,
, 请你用文字和公式写出计算A、C之间距离的步骤和结果.
请你用文字和公式写出计算A、C之间距离的步骤和结果.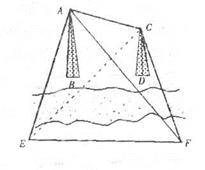
 是锐角三角形,
是锐角三角形, 分别是内角A、B、C所对边长,并且
分别是内角A、B、C所对边长,并且 .
. ;
; ,且
,且 ,求边
,求边 .
.