题目内容
设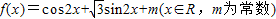 ,
,(1)求f(x)的最小正周期;
(2)若
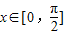 时,f(x)的最小值为4,求m的值.
时,f(x)的最小值为4,求m的值.
【答案】分析:(1)由已知中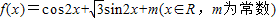 ,利用辅助角公式,我们易将函数解析式化为正弦型函数的形式,求出ω值后,代入T=
,利用辅助角公式,我们易将函数解析式化为正弦型函数的形式,求出ω值后,代入T=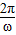 ,即可求出(x)的最小正周期;
,即可求出(x)的最小正周期;
(2)由已知中 ,根据正弦型函数的性质,我们易求出当
,根据正弦型函数的性质,我们易求出当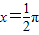 时,f(x)取最小值4,由此易构造一个关于m的方程,解方程即可求出m的值.
时,f(x)取最小值4,由此易构造一个关于m的方程,解方程即可求出m的值.
解答:(1)∵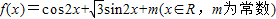 ,
,
∴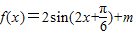
即ω=2
所以T=π.(5分)
(2)∵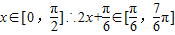 ,
,
∴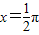 时,f(x)min=
时,f(x)min=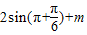 =-1+m=4,
=-1+m=4,
∴m=5(5分)
点评:本题考查的知识点是三角函数的周期性及其求法,三角函数的最值,其中利用辅助角公式,将函数的解析式化为正弦型函数的形式是解答的关键.
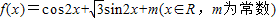 ,利用辅助角公式,我们易将函数解析式化为正弦型函数的形式,求出ω值后,代入T=
,利用辅助角公式,我们易将函数解析式化为正弦型函数的形式,求出ω值后,代入T=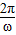 ,即可求出(x)的最小正周期;
,即可求出(x)的最小正周期;(2)由已知中
 ,根据正弦型函数的性质,我们易求出当
,根据正弦型函数的性质,我们易求出当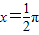 时,f(x)取最小值4,由此易构造一个关于m的方程,解方程即可求出m的值.
时,f(x)取最小值4,由此易构造一个关于m的方程,解方程即可求出m的值.解答:(1)∵
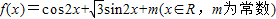 ,
,∴
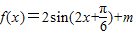
即ω=2
所以T=π.(5分)
(2)∵
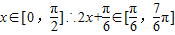 ,
,∴
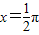 时,f(x)min=
时,f(x)min=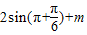 =-1+m=4,
=-1+m=4,∴m=5(5分)
点评:本题考查的知识点是三角函数的周期性及其求法,三角函数的最值,其中利用辅助角公式,将函数的解析式化为正弦型函数的形式是解答的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
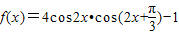 .
.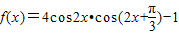 .
.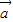 =(sinx,
=(sinx,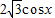 ),
),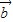 =(2sinx,sinx),设
=(2sinx,sinx),设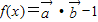 ,
, ,求f(x)的值域;
,求f(x)的值域;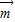 =(t,0)作长度最短的平移后,其图象关于原点对称,求
=(t,0)作长度最短的平移后,其图象关于原点对称,求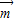 的坐标.
的坐标.